运算放大器分析----虚短和虚断（转载）

面对模拟电路中各种公式，若是不掌握本质内容，即使知道公式，哪天换一种模式，可能就不会算了。本节主要讲解运算放大器的计算。 运算放大器两板斧：“虚短”，“虚断”； 虚短：在分析运算放大器处于线性状态时，可把两输入端视为等电位，这一特性称为虚假短路，简称虚短； 虚断：在分析运放处于线性状态时，可以把两输入端视为等效开路，这一特性称为虚假开路，简称虚断。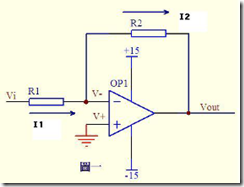 图15.8 反向放大电路

图15.8运放的同向端接地=0V，反向端和同向端虚短，所以也是0V，反向输入端输入电阻很高，虚断，几乎没有电流注入和流出，那么R1和R2相当于是串联的，流过一个串联电路中的每一只组件的电流是相同的，即流过R1的电流和流过R2的电流是相同的。 流过R1的电流I1 = (Vi - V-)/R1  （a） 流过R2的电流I2 = (V- - Vout)/R2 （b） V- = V+ = 0  （c） I1 = I2 （d） 求解上面的初中代数方程得： Vout = (-R2/R1)*Vi 这就是传说中的反向放大器的输入输出关系式了。

图15.9 同向放大电路 Vi与V-虚短，则 ： Vi = V- （a） 因为虚断，反向输入端没有电流输入输出，通过R1和R2 的电流相等，设此电流为I，由欧姆定律得： I = Vout/(R1+R2)  （b） Vi等于R2上的分压， 即： Vi = I*R2  （c） 由上述各式得 Vout=Vi*(R1+R2)/R2 这就是传说中的同向放大器的公式了。

图15.10 加法放大电路 图15.10中，由虚短知： V- = V+ = 0  （a） 由虚断及基尔霍夫定律知，通过R2与R1的电流之和等于通过R3的电流，故 (V1 – V-)/R1 + (V2 – V-)/R2 = (V- – Vout)/R3  （b） 代入（a）式，（b）式变为 V1/R1 + V2/R2 = Vout/R3； 如果取R1=R2=R3，则上式变为 Vout= —（V1+V2）； 这就是传说中的加法器了。

图15.11 加法放大电路 请看图15.11。因为虚断，运放同向端没有电流流过，则流过R1和R2的电流相等，同理流过R4和R3的电流也相等。故 (V1 – V+)/R1 = (V+ - V2)/R2  （a） (Vout – V-)/R3 = V-/R4  （b） 由虚短知： V+ = V-  （c） 如果R1=R2，R3=R4，则由以上式子可以推导出 V+ = (V1 + V2)/2 V- = Vout/2 故 Vout = V1 + V2 也是一个加法器。

图15.12 积分放大电路 由虚短知，反向输入端的电压与同向端相等，由虚断知，通过R1的电流与通过C1的电流相等。通过R1的电流 i=V1/R1； 通过C1的电流 i=C*dUc/dt=-C*dVout/dt ； 所以: Vout=((-1/(R1*C1))∫V1dt； 输出电压与输入电压对时间的积分成正比,这就是传说中的积分电路了。若V1为恒定电压U，则上式变换为 Vout = -U*t/(R1*C1) （t 是时间），则Vout输出电压是一条从0至负电源电压按时间变化的直线。

图15.13 微分放大电路 图15.13中由虚断知，通过电容C1和电阻R2的电流是相等的，由虚短知，运放同向端与反向端电压是相等的。则： Vout = -i * R2 = -(R2*C1)dV1/dt 这是一个微分电路。如果V1是一个突然加入的直流电压，则输出Vout对应一个方向与V1相反的脉冲。

图15.14 差分放大电路 由虚短知： Vx = V1  （a） Vy = V2  （b） 由虚断知，运放输入端没有电流流过，则R1、R2、R3可视为串联，通过每一个电阻的电流是相同的， 电流 I=(Vx-Vy)/R2  （c） 则： Vo1-Vo2=I*(R1+R2+R3) = (Vx-Vy)(R1+R2+R3)/R2  （d） 由虚断知，流过R6与流过R7的电流相等,若R6=R7， 则 Vw = Vo2/2  （e） 同理若R4=R5，则 Vout – Vu = Vu – Vo1，故 Vu = (Vout+Vo1)/2  （f） 由虚短知， Vu = Vw  （g） 由（e）（f）（g）得 Vout = Vo2 – Vo1  （h） 由（d）（h）得 Vout = (Vy –Vx)(R1+R2+R3)/R2 上式中(R1+R2+R3)/R2是定值，此值确定了差值(Vy –Vx)的放大倍数。这个电路就是传说中的差分放大电路了。