摘要：

目前，随着光通信向高速率(速度>40Gb/s)发展以及激光加工的普及，市场上对瞬时大功率，高重复频率且稳定的激光的需求越来越大，其中以半导体激光器为泵浦源，掺杂光纤为增益介质的光纤激光器因其输出功率高(泵浦能量低)，重复频率高[通过利用群速度 {MOD}散（GVD)和非线性自相位调制(SPM),能产生接近傅里叶变换极限的光孤子脉冲]，成本低，低损耗(在1.55um处损耗已降为0.22dB/km)，光束质量好(光束衍射倍率因子M^2<1.05),体积小(无需水冷散热装置)，寿命长等优势而被广泛应用。基于此实际应用考虑，将锁模技术与光纤激光器相结合的技术收到普遍关注。本篇文章将就锁模光纤激光器的基本原理进行阐述，分析以及数值仿真。

---

基本原理：

锁模光纤激光器的结构一般由半导体激光器(泵浦源)，掺杂光纤(增益介质),谐振腔(一般为F-P谐振腔或环形谐振腔)，输出耦合器和锁模调制器构成，其中与一般光纤激光器不同且最重要的便是锁模调制器。结构如图所示：
综合考虑掺杂光纤的增益带宽，振荡阈值和F-P谐振腔的振荡模式选择，光纤中将产生有限个振幅不等的纵模(纵模间距相同)。其结果如图所示：
其各个纵模之间相位无关系，总的输出光强为所有纵模电矢量的加和，其最终结果导致振幅呈非周期，无规律波动，此时称为多模自由振荡模式，没有什么实用价值。如果我们通过某些方法使得各个相邻纵模之间的相位差为一定值，我们可以得到总的电矢量为:

其中2M+1为振荡纵模数，W0为中心角频率，ΔW为纵模间隔，a为相邻纵模位相差。此时纵模输出为锁模模式。两种模式的时域对比图如图所示：

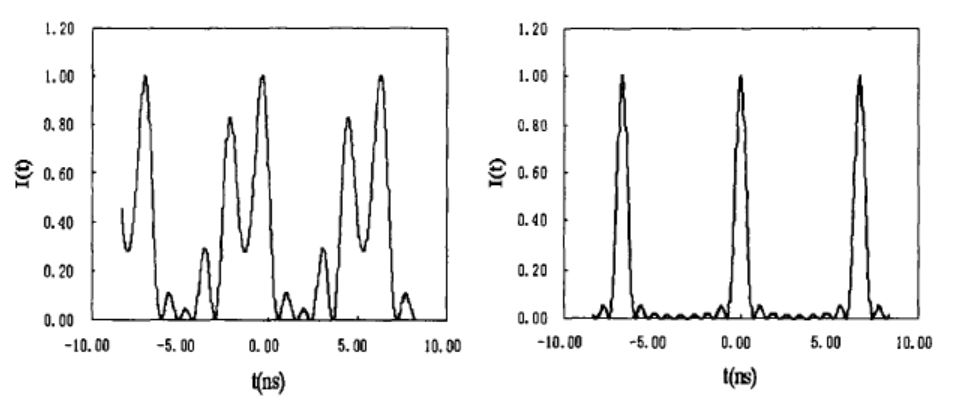
我们可以得到，脉冲周期为光在谐振腔类往返一次的时机的倒数，脉宽近似为振荡线宽的倒数(稍小于增益线宽),其输出峰值功率是多模自由振荡模式平均功率的2M+1倍。综述所述，我们可以通过锁模来得到高峰值功率，窄脉宽的周期光脉冲。

---

锁模分类：

光纤激光器中的锁模方法大致分为3种：
1.主动锁模；2.被动锁模；3.混合锁模
主动锁模：
主动锁模是通过外界信号来周期性调制谐振腔参数，从而达到纵模位相差恒定。在谐振腔类加入调制器，以等于纵模间隔的频率进行调制，使被调制纵模产生边频，达到与相邻纵模之间的位相差恒定。我们以幅度调制(FM)为例进行阐述:我们使用基于M-Z干涉仪的波导型LiNbO3电光振幅调制器(减少耦合损耗)。假设增益谱线中心频率的纵模首先振荡，则其被调制后电矢量为：

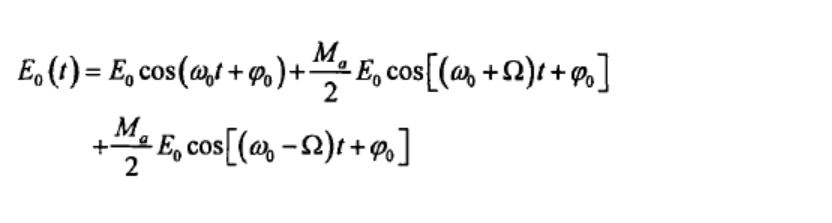
其中，Ma为调幅系数，可以看出受调制后，还产生了角频率相差为纵模间隔，相位差恒定的两个边频，以此同理，新产生的边频还将产生新的边频，直至产生所有纵模，且位相差为定值，满足锁模要求。
主动锁模光纤激光器优点是重复频率高，中心波长可调谐，易于实现高次谐波脉冲锁模，且脉冲为无频率啁啾的接近傅里叶变换极限的孤子脉冲。但缺点却也很致命：脉冲宽度较大(ps级)，易受环境影响，输出脉冲不稳定，成本高，无法实现全光纤结构，需要通过复杂的负反馈技术来保持脉冲稳定输出。
被动锁模：
被动锁模不需要在光纤中加入调制器，其基本原理是利用光纤中的非线性效应(主要是SPM)对输入脉冲强度的依赖性，其效果可以等效为饱和吸收体效应，即等效为一种特殊材料，它对较大的光强有较小的吸收系数，对较小的光强有较大的吸收系数，从而导致光强大处光强增加，光强小处光强减少，从而实现对光脉冲的窄化。就其实现方法上可以从两个方向上寻求突破，其一是寻找等效具有该效应的新的材料，如石墨烯等。其二是利用理论进行计算分析设计出具有等效的饱和吸收体效应的光路结构。考虑到我对材料学方面的一窍不通，我选择研究光路结构并分析。这其中的典型传统结构包括：非线性光纤环形镜，基于非线性偏振旋转效应的被动锁模(稍后讨论)等等。
其优点是脉宽窄，可实现全光纤集成，能够长久稳态运行，缺点是重复速率较低。
混合锁模
在激光器中同时使用主动和被动锁模，同时吸取二者的长处，能够产生窄脉宽，高重复频率且稳定的脉冲，但二者的缺点却也依然存在。

---

理论分析模型：

这部分是我这篇文章的重点，涉及到大量的理论知识与数学，可能对于一些人可能会不屑一顾，但我认为这恰是光纤激光器学习中最重要也最基础的部分，此后所有的光路结构都可以从这里加以修正进行数值分析仿真，同时也涉及一些最基础的光纤光学的概念。考虑到光纤光学过于复杂，短时间类难以方方面面涉及掌握，我主要针对一些我认为最重要，最核心的进行学习，当然学的也是相当不彻底，见谅。具体可以参考光纤光纤的权威之作：Agrawal的《非线性光纤光学原理及应用》，一共550页，够看一年了。。。
基本概念：
1） {MOD}散：(广义的 {MOD}散)
{MOD}散在光纤中往往是不可避免，但我们又尽量不希望 {MOD}散的存在，因为 {MOD}散总是导致光脉冲的展开，从而导致码间串扰，大大限制了通信速度。
对于光纤，主要由一下四种 {MOD}散：
模式 {MOD}散，材料 {MOD}散，波导 {MOD}散，偏振模 {MOD}散。
模式 {MOD}散：是指不同模式的光入射，因传播防暑不同而产生的 {MOD}散，考虑到目前大容量，高速率通信中大都采用单模光纤，模式 {MOD}散就无需考虑了。
材料 {MOD}散：不同波长的光对应的折射率不同导致的速度的不同，这是传统的 {MOD}散的定义。
波导 {MOD}散：不同波长的光在全反射时，有倏逝波的存在，导致不同波长的光将进入包层中不同深度后才返回光纤中，从而在效果上导致各个波长的光的速度不同。
材料 {MOD}散和波导 {MOD}散合称 {MOD}度 {MOD}散，二者作用可以相互抵消，例如对于波长在1.31um的光纤，其 {MOD}度 {MOD}散为0。
偏振模 {MOD}散：由于光纤本身材料的不对称性或缺陷，或者由于光纤受到非均匀应力，发生了光测弹性效应，从而使光纤变成了各向异性介质(单轴晶体)，从而发生了双折射效应。沿X与Y轴的偏振分量将产生相位差，从而导致脉冲展宽。偏振模 {MOD}散一般很小，但在高速通信中，对于 {MOD}度 {MOD}散为0的单模光纤，偏振模 {MOD}散将很大程度限制了光纤的发展。 {MOD}散通常有三种表示方式，分别为最大时延差(ps/km)， {MOD}散系数(ps/km*nm或ps^2/km)，光纤带宽(MHz*nm)，具体不展开了。
同时 {MOD}散往往存在高阶 {MOD}散，即K与W并非是线性关系。一般用泰勒级数在中心角频率W0的展开K(w)表示 {MOD}散。其中一阶系数B1为群速度倒数，二阶系数B2为群速度 {MOD}散参量(GVD),它在光纤光学中比较重要。B2>0为正常 {MOD}散，B2<0为反常 {MOD}散。往往反常 {MOD}散和非线性自相位调制能作用够相抵消互，形成稳定的孤子脉冲，后面我们将进行讨论。 2）非线性效应：
非线性效应是相当的复杂，比较常见的就有自相位调制(SPM),交叉相位调制(XPM)，四波混频(FWM)，受激拉曼散射(SRS)和受激布里渊散射(SBS)等，主要原因电偶极子极化强度与电场强度并不是简单的线性关系，这里不讨论了。就简单讨论下自相位调制作用。
在光强较大的情况下，折射率将随该光脉冲的光强变大而变大，即相位受到光强大小的调制，且为线性关系，从而波数k也将变化：B’=B+γP,P为光功率,γ为非线性系数，单位W^-1/km,大小范围1~10。
而交叉相位调制则是不同光脉冲，或不同偏振态的光脉冲受其他光脉冲的光强调制。其位相贡献是SPM的两倍。当光纤为单轴双折射晶体时我们往往需要考虑不同偏振态的脉冲之间的XPM效应。
SRS和SBS都是高阶非线性效应，一般只有光脉宽<100f或功率很大时才需考虑。本文章不考虑这些效应。 光脉冲传输方程：
从麦克斯韦方程组出发，使用慢变包络近似(即假设以光脉冲包络作为函数，忽略高阶导数，简化计算与推导）。
1）普通光纤:
我们可以得到如下方程：

这个就是著名的非线性薛定谔方程(NLS),当然是基于一定前提下得到的简化方程：不考虑拉曼散射，不考虑三阶及以上 {MOD}散效应，不考虑光纤损耗，脉宽<100fs。等式右边第一项为群速度 {MOD}散作用，第二项为非线性作用。
A.该方程使用群时延坐标系(即以群速度vg移动),T=t-z/vg,从而可以去除一阶 {MOD}散效应而只考虑二阶 {MOD}散效应。
B.变量做了归一化处理：τ=T/T0,T0为脉宽；ξ=z/Ld,Ld=T0^2/|B2|为 {MOD}散长度,z为脉冲传播长度；U(z,t)=A/√P0，A为电矢量振幅，P0为峰值功率;Lnl=1/γ,Lnl为非线性长度；Ld与Lnl分别表征GVD和SPM大小(越小作用越大)，N=√Ld/Lnl表征GVD和SPM那个影响大。
该偏微分方程难以接出解析解，我们需要对其进行数值分析。这里我们使用分步傅里叶变换算法(SSFT)。我们分别将群速度 {MOD}散作用与非线性作用分别用算符D与N表示，则将上述方程转化为常微分方程：

则该常微分方程解为:U=Cexp[(D+N)z]
我们将脉冲的传播过程分成一个个小间隔dz,再将dz分为h=dz/2。在该间隔内分别执行如下3个操作(使用对称分步傅里叶变换,其精度为步长的三次方，优于传统的SSFT）：
1.首先在前h内仅让GVD产生效果，得U(Z+h,t)=U(z,t)exp(D*h)。对该式进行傅里叶变换,可将U对t的二阶偏导利用傅里叶变换的性质变为(iw)^2,则:
F[D]=i/2*sgn(B2)*W^2;再用快速傅里叶变换求Ut的傅里叶变换F[Ut]，则更新后的Ut的傅里叶变换为U(W)=F[Ut]*F[D]，再用傅里叶逆变换求出Ut。
2.接着，在dz内让SPM产生效果，得更新后的Ut=Ut*exp(N*2h)。
3.之后再重复步骤1，即可得到z+dz后的脉冲。
具体matlab程序如下： mmm=0.3;%衡量 {MOD}散作用大小 N=3;%描述GVD与SPM作用谁大 M=2^11;%时间序列大小 dz=0.01;%位置序列步长 B2=-20;%群速度 {MOD}散B2>0正常 {MOD}散，B2<0反常 {MOD}散 Tw=10;%时间长度 M1=M-1; dt=2*Tw/M1;%时间序列步长 Zw=mmm; h=dz/2;%分步傅里叶变换 {MOD}散作用单位步长 t=-Tw:dt:Tw;%时间序列 c=0;%啁啾系数 Uin=exp(-t.^2/16).*exp(-1i*0.5*c*t.^2);%输入初始高斯型孤子序列(包括产生的啁啾效应) Iin=Uin.*conj(Uin);%光强序列 Fs=1/dt;%取样频率 df=Fs/M1;%取样频率间隔/分辨率(同时域间隔) dw=2*pi*df;%取样角频率 Ws=2*pi*Fs;%取样角频率间隔 w=0:dw:Ws;%取样角频率序列 Mm=M/2; w1=0:dw:Mm*dw; w2=(Mm-1)*dw:-dw:dw; ww=[w1 w2]; %判断正常 {MOD}散还是反常 {MOD}散 if B2>=0%正常 {MOD}散 sgn=1; else %反常 {MOD}散 sgn=-1; end Dw=1i*sgn*0.5*ww.^2;% {MOD}散算子的傅里叶变换 Mw=exp(Dw*h);%孤子行走h后 {MOD}散产生的影响因子 t0=t; nn=1; Ut=Uin; ttt=floor((Zw-dz)/dz);%步长序列 U=zeros(ttt+1,length(t)); zzz=dz:dz:Zw; for z=dz:dz:Zw Uw=fft(Ut);%归一化振幅函数的傅里叶变换 Uw=Mw.*Uw;%行走h后在 {MOD}散作用下新孤子脉冲波形的傅里叶变换频谱 Ut=ifft(Uw);%傅里叶逆变换，得到新的时域脉冲函数 Nt=1i*N^2*(Ut.*conj(Ut));%非线性算子 Mt=exp(Nt*dz);%孤子行走2h后 {MOD}散产生的影响因子->对称分步傅里叶变换法，减少误差 Ut=Mt.*Ut;%新的在非线性作用下的脉冲时域图 Uw=fft(Ut);%新孤子时域图函数的傅里叶变换 Uw=Mw.*Uw;%行走h后在 {MOD}散作用下新孤子脉冲波形的傅里叶变换频谱 Ut=ifft(Uw);%傅里叶逆变换，得到dz=2h步长下的更新的时域脉冲函数 I=Ut.*conj(Ut);%时域脉冲光强 U(nn,:)=I; nn=nn+1; end mesh(t,zzz,U)%画三维图 xlabel('Time') ylabel('distance') zlabel('light intensity') title('the influnce of GVD and SPM') 我们对GVD与SPM对脉冲的整形作用进行讨论(假设代码是对的)：
(1)N=1，B2=-20，mm=0.1。此时GVD(反常 {MOD}散)与SPM作用相互抵消，脉冲在传播过程中几乎不发生变形，如下图所示：

(2)mm=0.02，此时GVD与SPM作用很小，无论N为多少(即无论哪个效应作用大),脉冲形状也基本不变。其图像仍如上图所示
(3)mm=0.8,N=8,B2=20时，此时为正常 {MOD}散且GVD效果远大于SPM效果，将会发生脉冲展宽，且N越大，脉冲展宽越明显。其图像如下图所示：

(3)mm=0.8,N=4,B2=-20时，此时为反常 {MOD}散且GVD效果远大于SPM效果，将会开始也发生脉冲展宽，但是当mm=z/Ld>0.3后将发生脉冲压缩;再之后，当z/Ld>0.5后，脉冲将发生分裂，分裂成2个振幅相等的脉冲，之后2个脉冲继续发生分裂，最后形成脉冲间隔近似相等，振幅不等的几个脉冲。脉冲个数随N与mm的增大而增大。如下图所示：

(4)mm=0.5,B2=-20,N=3，脉冲将发生压缩，同时综合(3)和(4)，如果GVD效果较大，且GVD与SPM作用效果差的不是很大，则不会导致脉冲分裂发生。如下图所示：

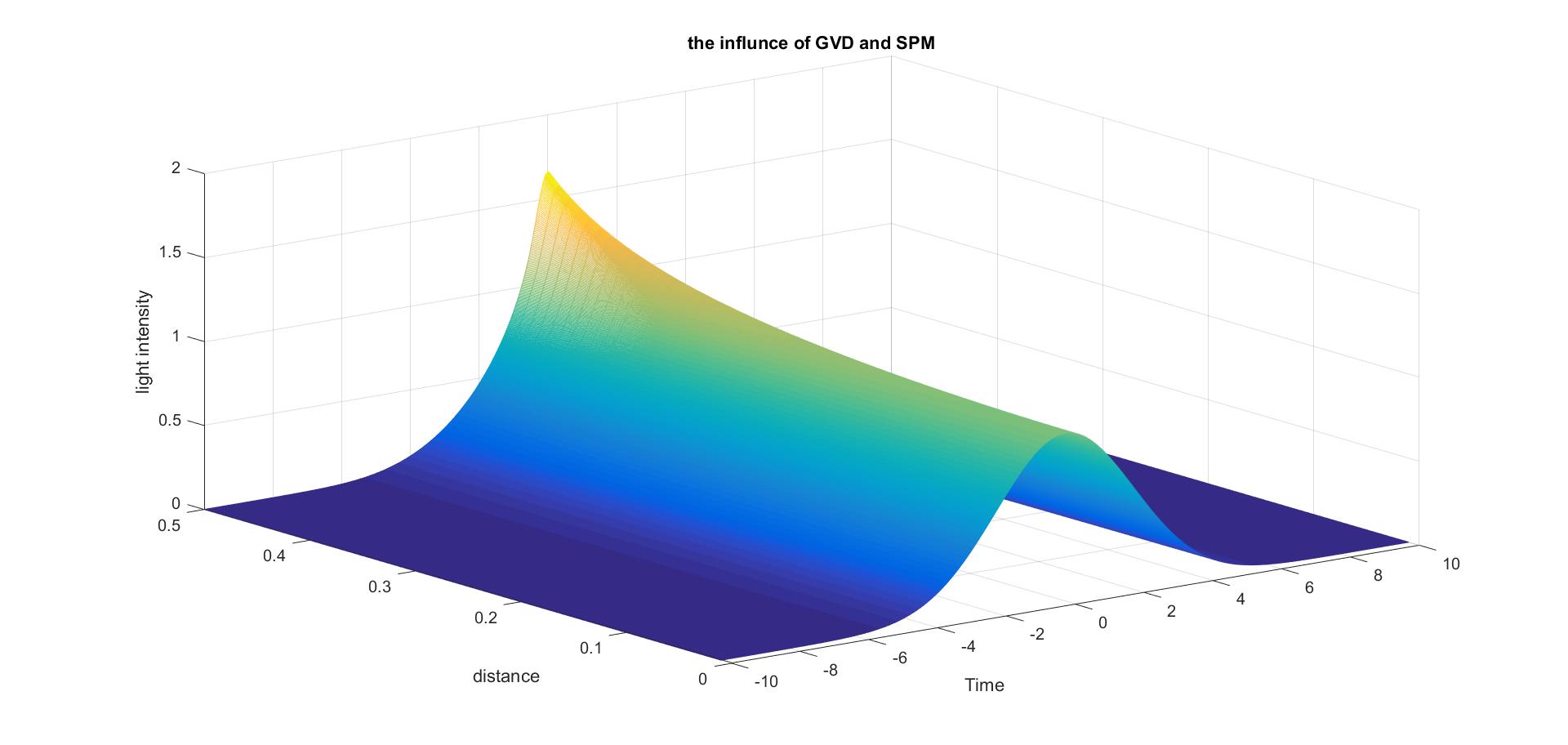
上述结果可能有误。。。 以上讨论的是在普通光纤上的脉冲传播情况，如果是掺杂增益光纤，还需考虑随光强变化的增益系数，我们将得到由U(z,t)与增益系数g(z,t)两个相互关联的函数构成的偏微分方程组。这里我们不做讨论。

---

基于非线性偏振旋转效应的被动锁模：

最传统的结构如下图所示：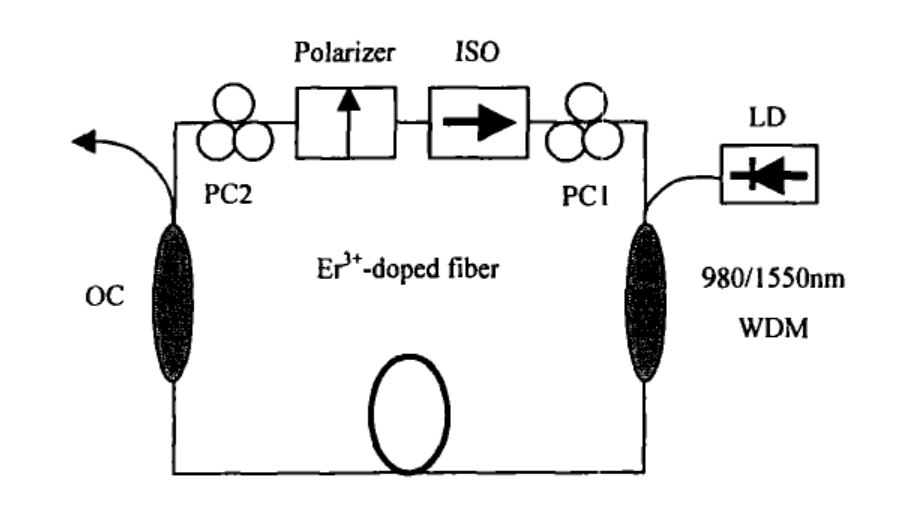

我们使用980nm的半导体激光器作为泵浦源，使用WDM(波分复用器)将泵浦光与光纤产生的1.55um光进行耦合。中间加入一定长度的掺铒增益光纤，使用9：1的输出耦合器OC，锁模调制元件由一个起偏器，两个偏振控制器(PC1,PC2)和一个光隔离器(ISO)构成。
其基本原理是：光脉冲进过偏振片变成线偏振光，线偏振光经偏振控制器变成椭圆偏振光，椭圆偏振光可以分解为两个振幅不同的左旋与右旋光(任何偏振光都可以分解为两个正交偏振光的线性叠加)。这两个圆偏振光收到SPM与XPM的作用，不同光强处将产生不同位移，叠加后偏振偏振状态(偏振旋转)发生改变，但偏振片再次通过时，会由于不同脉冲强度处偏振状态不同而产生一种自幅度调制作用的等效可饱和吸收体效应，从而实现脉冲的窄化。
调制元件分析：
我可以使用斯托克斯矢量与偏振器件的Muller矩阵(或使用琼斯矢量与矩阵)对其由偏振片，偏振控制器和双折射光纤构成的简化系统进行分析，分别得到其线性与非线性效应。具体分析计算略，仅给出如下结论：
1.要使环形腔发生多纵模运转，则起偏器方向应平行与光纤主偏振态方向且要调整偏振控制器使得入射光场平行与光纤主偏振态方向。
2.当改变入射到光纤主偏振态方向上的两个偏振光的相位差，可以使纵模可调谐。
3.要使激光能够输出稳定的锁模脉冲,要使偏振控制器透射率接近1。
腔体参数的影响：
使用时域动力学锁模方程更能分析腔体参数对锁模脉冲的影响，这里同样不给出理论(不会。。。)，仅给出部分结论：
1当自相位调制作用一定时：
1)位于反常 {MOD}散区的脉冲宽度要小于正常 {MOD}散区的脉冲，且更为稳定。
2)正 {MOD}散作用越大，脉宽越大，脉冲啁啾也越大；反常 {MOD}散越大，脉冲啁啾趋于0。
2当自幅度调制作用一定时：
1)在正常 {MOD}散区，自相位调制作用γ对脉宽与脉冲啁啾影响较大，γ越大，脉宽与脉冲啁啾越大；在反常 {MOD}散区，γ对脉宽与脉冲啁啾影响不大。
2)当γ较小时，在反常 {MOD}散区，脉冲无法稳定，需要增大反常 {MOD}散来保持脉冲稳定与减少脉冲频率啁啾。
被动锁模自启动分析：
我们希望激光器能够不受外界调制即可输出稳定的锁模脉冲，我们使用增益光纤的广义路径平均非线性薛定谔方程进行分析(分布增益与分布损耗模型)：

其中g为增益光纤的路径平均增益系数,我们将掺杂光纤利用路径平均等效为均匀增宽介质，则有g=g0/(1+p/pm)，其中g0为小信号增益，p为脉冲一个周期内的平均光功率，pm为饱和光功率；a=0.3dB/km为光纤损耗，Bf=20nm为增益带宽,D=-B2/2=-10ps^2/km，γ3=0.39,γ5=0.12为饱和吸收体效应的三阶与五阶非线性系数,γ=2.6。仍使用SSTF算法进行数值仿真。并对不同增益系数下的自启振状态进行讨论：
1.当g0<=a时，激光器无法起振，无激光输出。
2.当g0>a且较小时，只能产生连续波激光输出，无法产生锁模脉冲。
3.当g0较大时，激光先输出连续波，稍后逐步演化成稳定锁模脉冲。
4.当g0很大时，激光将直接缓慢生成锁模脉冲并不断压缩脉宽并稳定。
综上，我们知道要想生成稳定锁模脉冲，需要有较大的小信号增益系数与较大功率的泵浦光。

---

后续工作：

1.进入实验室，熟悉相关操作与仪器的使用。进行简单的光纤激光器的搭建工作。
2.搭建基于非线性偏振旋转效应的被动锁模光路，并改变参数进行实验，验证理论分析，并尝试发现新的研究现象。
3.深入学习非线性光纤学习，加深对相应概念与SSFT算法的理解与应用。
4.学习高次谐波锁模脉冲的机制，并进行仿真与实验验证。发现其不足与缺陷。
5.查阅更多资料，寻找更多改进结构以产生10GHz重复频率的脉冲。
6.理论分析，参考，争取构造新的结构，建模验证分析。
7.搭建光路结构，实验验证，发现新的现象，并力求能够进行解释。
8.学习总结，实验汇总。
9.论文撰写，修改，投稿->SCI/IEEE等。

---

参考文献：

[1]贾东方，余震虹等译，Govind.P.Agrawal著，非线性光纤光学原理及应用.电子工业出版社，2002.
[2]梁铨廷著，物理光学.电子工业出版社，2012.
[3]陈家壁，彭润玲著，激光原理及应用.电子工业出版社，2009.
[4]顾畹仪，黄永清等著，光纤通信.人民邮电出版社，2011.
[5]原荣，邱琪著，光子学与光电子学.机械工业出版社，2014.
[6]吴湘淇著，信号与系统.电子工业出版社，2009.
[7]赵德双.高性能锁模光纤激光器研究[D].电子科技大学,2005.
[8]陶莎.高重复频率被动锁模光纤激光器的研究[D].中国科学技术大学,2016. P.S：这篇文章算是几乎奠定了我向光电子方向发展的趋势，计划今后从器件与光路结构两个方面学习相应知识，同时渗透学习电子技术，涉及通信,信号，高频，电磁波微波，FPGA,单片机控制等方面。有空接触一下物理材料方面的知识，诸如半导体物理，固体物理学等，还有相应的元器件方面的制造，制造，封装，测试技术等等。。。 耽误了一年的时间去水比赛，现在终于要回归了！
加油！！！