补码这个概念从开始学的时候就一直记不住到底是怎么运算,看一次忘一次。备考时又拿出来看到了,这次就好好看看为什么会有补码、补码为什么叫补码、补码是干什么的。
在观察颜 {MOD}的时候,补 {MOD}会随时随地的跟着主 {MOD}的出现而产生。我们可以发现补 {MOD}会让主 {MOD}更加地明显。就像黑 {MOD}和白 {MOD}单独存在时,并不会显得白的很白、黑的很黑,但是如果将两者放在一起,就会有白的很白、黑的很黑的现象。而且补 {MOD}还可以避免视觉对主 {MOD}长期观看后产生疲劳,比如做手术的大夫穿绿 {MOD}手术服,是因为手术中有大量红 {MOD}的血,人看久了就会怠慢,从而延误手术。青绿 {MOD}是红 {MOD}的补 {MOD},大夫穿上了青绿 {MOD}手术服,手术中看到红 {MOD},也看到青绿 {MOD},从而避免怠慢。
说白了,“补”这个概念不是单独存在的。当提到两个相对应的事物时,若把一方称为“主”,那么对应的一方就称为“补”。我们找出这个称之为的“补”的事物来,是为了更好的认识称之为“主”的事物。
GOOGLE时,看到豆瓣的一篇文章。我们需要用计算机完成运算。但是计算机中只有加法器,当我们想做减法时没有减法器来让计算机直接知道减法的结果。为了解决这个问题,补码出现了。
数字 87,减去 25,和加上 75,在不考虑百位数的条件下,效果也是相同的。
上述几组数字,有这样的关系:
3+9=12
60 + 300 = 360
25 + 75 = 100
式中的 12、360 和 100,就是“模”。
式中的 3 和 3、60 和 300,以及 25 和 75,就是一对对“互补”的数字。 知道了“模”,求某个数字的“补数”,就是轻而易举的了:
如果模为 365,数字 120 的补数为:365 - 120 = 245。 用补数代替原数,可把减法转变为加法。出现的进位就是模,此时的进位,就应该忽略不计。
对于6-3=6+(12-3)。在有模的前提下,我们去掉6,得到:
这样就给我们在计算机中做减法提供了一个良好的思路。
那么当 8 位二进制数参加运算,模就是 1 0000 0000(2^8),即 1 的后面加上 8 个 0。
16 位二进制数参加运算,模可就大了,是 1 的后面加上 16 个 0。
前面我们说了补码的提出是为了解决减法计算的问题。所以在计算时,加法运算我们仍然按照原来的机器码(原码)进行计算。
我们一般是在8位二进制的情况下讨论补码。
例如-3的原码是10000011,其绝对值的原码是00000011。那么-3的补码就是100000000-00000011=11111101。 应用补码进行计算
用补码计算:83-25=58。 83 ---都变成补码,再用加法运算--> 0101 0011
- 25 -> 1 0000 0000 - 0001 1001-> + 1110 0111
----- --------
58 <--忽略进位1,结果就是正确的--[1] 0011 1010 计算正确的前提是参与运算的数字不能大于模。若是大于模,模也需要变大。
补 {MOD}
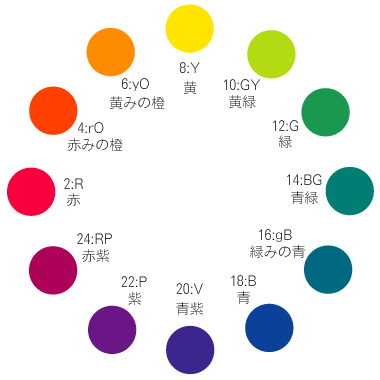
在解决这些问题之前,我们先来谈谈补码的这个“补”字。说起“补”,会想起以前美术课上学过的补 {MOD}。所谓补 {MOD},就是 {MOD}相环上相距180°的 {MOD}相。就像下图上“黄”和“青紫”互为补 {MOD}。
说白了,“补”这个概念不是单独存在的。当提到两个相对应的事物时,若把一方称为“主”,那么对应的一方就称为“补”。我们找出这个称之为的“补”的事物来,是为了更好的认识称之为“主”的事物。
为什么需要补码
知道了“补”这个字的含义之后,我们就可以来看看计算机是如何利用“补”的含义来完成一些极其重要的任务的。GOOGLE时,看到豆瓣的一篇文章。我们需要用计算机完成运算。但是计算机中只有加法器,当我们想做减法时没有减法器来让计算机直接知道减法的结果。为了解决这个问题,补码出现了。
模和补数
假如现在是6点,想知道3个小时前是几点,我们可以直接把时针逆时针旋转3个小时,也可以顺时针旋转9个小时,得到的时间是一样的。用数学语言我们可以这样表示:6 - 3 = 6 +(12 - 3)
还有,我们可以发现把物体左转60度,和把物体右转300度的结果也是一样的。 数字 87,减去 25,和加上 75,在不考虑百位数的条件下,效果也是相同的。
上述几组数字,有这样的关系:
3+9=12
60 + 300 = 360
25 + 75 = 100
式中的 12、360 和 100,就是“模”。
式中的 3 和 3、60 和 300,以及 25 和 75,就是一对对“互补”的数字。 知道了“模”,求某个数字的“补数”,就是轻而易举的了:
如果模为 365,数字 120 的补数为:365 - 120 = 245。 用补数代替原数,可把减法转变为加法。出现的进位就是模,此时的进位,就应该忽略不计。
对于6-3=6+(12-3)。在有模的前提下,我们去掉6,得到:
-3=12-3。
我们可以把减法理解成加一个负数。于是我们在计算减法时只要加上模减去这个负数的绝对值就可以得到正确的结果。 这样就给我们在计算机中做减法提供了一个良好的思路。
二进制的模
十进制下,两位数的模是100,三位数的模是1000,n位数的模式10^n。在二进制下,我们可以发现两位数的模是100(十进制的4)。模表示数字的容量和状态,两位二进制能表示4个数。所以可以推出,n位二进制的数的模式2^n,也就是1后面有n个0。 如果是 3 位二进制数参加运算,模就是 1000(2^3),即 1 的后面加上 3 个 0;那么当 8 位二进制数参加运算,模就是 1 0000 0000(2^8),即 1 的后面加上 8 个 0。
16 位二进制数参加运算,模可就大了,是 1 的后面加上 16 个 0。
二进制的补码
在计算机里,数字、字符串等等会被称为“码”,还有机器码。那么补数也就变个称呼,显得专业一点,我们称之为补码。前面我们说了补码的提出是为了解决减法计算的问题。所以在计算时,加法运算我们仍然按照原来的机器码(原码)进行计算。
我们一般是在8位二进制的情况下讨论补码。
例如-3的原码是10000011,其绝对值的原码是00000011。那么-3的补码就是100000000-00000011=11111101。 应用补码进行计算
用补码计算:83-25=58。 83 ---都变成补码,再用加法运算--> 0101 0011
- 25 -> 1 0000 0000 - 0001 1001-> + 1110 0111
----- --------
58 <--忽略进位1,结果就是正确的--[1] 0011 1010 计算正确的前提是参与运算的数字不能大于模。若是大于模,模也需要变大。
总结
- 首先“补”和“模”的概念适用于像 {MOD}相环、钟表这种有个环的事物,模就相当于那个环。十一点加一个小时就是零点,在8位二进制的数字中,11111111加1就是00000000。当你忘了补码的样子,就想一想钟表吧。正是有了模,才有所谓的补。
- 其次在二进制中,n位数的模就是2^n,也就是1后面有n个0。
- 负值在内存中以补码形式存贮
- 负数X的补码 = |X|按位求反+1
= X按拉求反(除符号位外)+1
= 模 - |X| (强调了补码运算本质上是一种模运算,这就是称其为“补码”的缘由) - -128的补码是10000000,等于128的原码。