在ROS的Cmake中使用Eigen库进行矩阵和向量的运算和很方便。下面逐步添加他的使用方法。
　　
１　配置
　　首先要在CmakeLists.txt中先进行设置：
由于Eigen是ros以外的库，所以要单独的使用
　　find_package(Eigen REQUIRED)
同时Eigen依赖cmake_modules。所以还要
　　find_package(catkin REQUIRED COMPONENTS
　　cmake_modules)。 2 认识一些头文件
Eigen库分为 核心模块和额外模块两部分，每个模块都有一个用这个模块所相对应的头文件，Eigen和Dense头文件方便的同时包含了几个头文件以供使用。下面做简单介绍：
——Core
有关矩阵和数组的类，有基本的线性代数（包含 三角形 和 自伴乘积 相关），还有相应对数组的操作。
——Geometry
几何学的类，有关转换、平移、进位制、2D旋转、3D旋转（四元组和角轴相关）
——LU
逻辑单元的类，有关求逆，求行列式，LU分解解算器（FullPivLU,PartialPivLU)
——Cholesky
包含LLT和LDLT的乔里斯基因式分解法。
（小科普：Cholesky分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解）
——Householder
豪斯霍尔德变换，这个模块供几个线性代数模块使用。
（Householder transform: 维基百科 ）
——SVD
奇异值分解，最小二乘解算器解决奇异值分解。
——QR
QR分解求解，三种方法：HouseholderQR、ColPivHouseholderQR、FullPivHouseholderQR
——Eigenvalues
特征值和特征向量分解的方法：EigenSolver、SelfAdjointEigenSolver、ComplexEigenSolver
——Sparse
稀疏矩阵相关类，对于稀疏矩阵的存储及相关基本线性代数
——Dense
包含： Core、Gelometry、LU、Cholesky、SVD、QR和Eigenvalues模块（头文件）
——Eigen
包含上述所有的模块（头文件） 3 矩阵简单操作
Eigen提供了两种密集的对象Matrix（矩阵）和Vector（向量）。
这两者是通过矩阵模板类和一维或二维的数组模板类来实现的。
这两者有几点不同：
——Matrix类型变量加减法，若行列数不相等，则不能做加减；
Array类型的可以加减一个常数（各个元素分别加减该常数）。
——Matrix与Array类型变量做乘法也会有不同，Matrix是矩阵相乘，Array是对应元素相乘。
——但两者可以相互转换，方法为 .array() 和 .matrix()。
3.1 定义
定义矩阵时，默认没有初始化，必须自己初始化。
Eigen的矩阵类型，一般是Matrix后面跟类型符号来表示，比如说：
——’ d ’ 代表 double，矩阵存储的是double型的数据
——’ f ’ 代表float，矩阵存储的是float类型数据
——’ c ‘代表complex，矩阵存数的是复数类型数据
——’ i ‘代表int，矩阵存储的是整数类型
相应关系为：

3.2 初始化 m1=MatrixXf::Zero(3,4); // 将矩阵3行4列初始化为0 m2=MatrixXf::Ones(3,3); // 将矩阵3行3列初始化为1 v1=Vector3f::Ones(); // 将3行的纵向量初始化为1 cout<<"m1= "<<m1<<endl; cout<<"m2= "<<m2<<endl; cout<<"v1= "<<v1<<endl; 运行结果为：
3.3 访问
直接就同数组的访问方式一样，但是不是方括号，而是圆括号： MatrixXf m3(2,3); m3<<1,2,3,4,5,6; cout<<"m3_1 "<// 为了美观点，更像个矩阵，可以换行写 m3<<1.3,4,-8, 0,0.9,2; cout<<"m3_2= "<// 将第2行第3列的值改为99 m3(1,2)=99; cout<<"m3_3= "< 当然，同数组一样，第一行第一列的下标为（0,0）
输出结果：
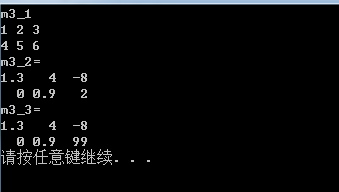4 矩阵的运算
——置0
——置1
——随机矩阵
——单位阵
——求逆
——转置
——数乘矩阵
——向量求模值
MatrixXf m1(3,3);
// 矩阵全部元素置0
m1.setZero();
cout<<"m1_1= "< // 矩阵全部元素置1 ( 这里行列值不填，默认定义时候的行列，
// 若填写，则矩阵也会更改为填写的行列值 )
m1.setOnes(2,2);
cout<<"m1_2= "< // 随机生成一个矩阵
m1.setRandom();
cout<<"m1_3= "< // 置单位矩阵
m1.setIdentity(3,3);
cout<<"m1_4= "< m1<< 1 , 2 , 3 ,
5 , 9 ,10 ,
7 , 0 ,1 ;
// 矩阵求逆
m1.inverse();
cout<<"m1_5= "< // 矩阵转置
m1.transpose();
cout<<"m1_6= "< // 数 * 矩阵 ( 数 / 矩阵 )
m1 = 2.6 * m1 ;
cout<<"m1_7= "< //求向量模值 norm() 待更新。。。。。
参考：
http://blog.csdn.net/lttree/article/details/39099315