你需要花多少时间来计算下面这道题目呢?
123456789 * 987654321 = ()
A. 121932631112635266 B.121932631112635267
C.121932631112635268 D.121932631112635269
既然是选择题,不必费力把答案完整的计算出来,4个选项的个位数都不相同,因此只需要计算是出答案的最后一位即可,不难得出,它等于1*9=9.把刚才的解题过程抽象出来就是下面的式子:
123456789 * 987654321 mod % 10 = ((123456789 mod 10) * (987654321 mod 10)) mod 10
其中a mod b表示a 除以 b 的余数,C语言表达式是a % b。在本章中,b一定是正整数,尽管b < 0 时表达式a % b也是合法的(但b=0时)会出现除零错)。
不难得到下面的公式:
(a+b)%n=(a%n+b%n)%n
(a-b)%n=(a%n-b%n+n)%n;
ab%n=(a%n * b%n)%n 注意在减法中,由于a mod n可能小于b mod n,需要在结果加上n,而在乘法中,需要注意a mod n和 b mod n相乘是否会溢出。 例如:当n=10^9时,ab mod n一定在int范围内,但a mod n 和 b mod n 的乘积可能会超过int。需要用long long保存中间结果。 求a * b mod n: 输入:整数a,b,n。 输出:a * b mod n. 运行结果: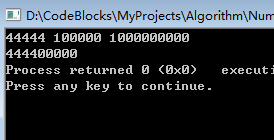
 首先,把大整数写成自左向右的形式,1234=((1*10+2)*10+3)*10 + 4,然后用前面的公式,每步取模。
此处困惑了我好久,一直不明白这个方式是用前面的几个公式如何推导出来的。最后看了别人博客才明白:
取模运算:模拟手算竖式的方法。用x从高到低的每一位加上前一位余数*10来对bi进行%,最后得到的结果就是x%bi的结果。
利用到公式:(a+b) mod (n) = (a mod n) + (b mod n) mod (n);
参考自: 大整数取模
明白了思路后,代码也就明白了。
首先,把大整数写成自左向右的形式,1234=((1*10+2)*10+3)*10 + 4,然后用前面的公式,每步取模。
此处困惑了我好久,一直不明白这个方式是用前面的几个公式如何推导出来的。最后看了别人博客才明白:
取模运算:模拟手算竖式的方法。用x从高到低的每一位加上前一位余数*10来对bi进行%,最后得到的结果就是x%bi的结果。
利用到公式:(a+b) mod (n) = (a mod n) + (b mod n) mod (n);
参考自: 大整数取模
明白了思路后,代码也就明白了。
 不难写出下面的代码:
不难写出下面的代码:

(a-b)%n=(a%n-b%n+n)%n;
ab%n=(a%n * b%n)%n 注意在减法中,由于a mod n可能小于b mod n,需要在结果加上n,而在乘法中,需要注意a mod n和 b mod n相乘是否会溢出。 例如:当n=10^9时,ab mod n一定在int范围内,但a mod n 和 b mod n 的乘积可能会超过int。需要用long long保存中间结果。 求a * b mod n: 输入:整数a,b,n。 输出:a * b mod n. 运行结果:

int mul_mod(int n, int a, int b)
{
a %= n;
b %= n;
return (int)((long long)a * b % n); //防止溢出 中间用longlong
}
当然,如果n本身超过int但又在long long范围内。上述方法就不适用了,建议使用高精度乘法。
大整数取模。
输入:正整数n和m。 n<= 10^100, m<=10^9
输出:n mod m。
运行结果:
 首先,把大整数写成自左向右的形式,1234=((1*10+2)*10+3)*10 + 4,然后用前面的公式,每步取模。
此处困惑了我好久,一直不明白这个方式是用前面的几个公式如何推导出来的。最后看了别人博客才明白:
取模运算:模拟手算竖式的方法。用x从高到低的每一位加上前一位余数*10来对bi进行%,最后得到的结果就是x%bi的结果。
利用到公式:(a+b) mod (n) = (a mod n) + (b mod n) mod (n);
参考自: 大整数取模
明白了思路后,代码也就明白了。
首先,把大整数写成自左向右的形式,1234=((1*10+2)*10+3)*10 + 4,然后用前面的公式,每步取模。
此处困惑了我好久,一直不明白这个方式是用前面的几个公式如何推导出来的。最后看了别人博客才明白:
取模运算:模拟手算竖式的方法。用x从高到低的每一位加上前一位余数*10来对bi进行%,最后得到的结果就是x%bi的结果。
利用到公式:(a+b) mod (n) = (a mod n) + (b mod n) mod (n);
参考自: 大整数取模
明白了思路后,代码也就明白了。
void big_mod()
{
char n[110];
int i, m, len, ans;
ans = 0;
scanf("%s %d", n, &m);
len = strlen(n);
for(i = 0; i < len; i++)
ans = (int)(((long long)ans*10 + n[i] - '0') % m);
printf("%d
", ans);
}
幂取模:
输入:正整数a、n和m。 a,n,m <= 10^9
输出:a^n mod m的值。
运行结果:
 不难写出下面的代码:
不难写出下面的代码:
void pow_mod(int a, int n, int m)
{
int i, ans;
ans = 1;
for(i = 0; i < n; i++)
ans = (int)((long long)ans * a % m);
printf("%d
", ans);
}
看上去似乎不满足公式 ab mod n = (a mod n)(b mod n) mod n.但是却满足 (a mod n)(b) mod n。这两者相等么?
答案是相等的。因为我发现这个式子可以写成:
(a mod n)(b) mod n = ((a mod n) mod n)(b mod n) mod n = (a mod n)(b mod n) mod n.
我们发现,正好就是我们的乘法取模公式。
这个函数的时间复杂度为O(n),当n很大时速度很不理想(注意运行结果里的时间高达50多秒)。有什么办法算的更快呢?
可以利用分治法。
运行结果:

int improvement_pow_mod(int a, int n, int m)
{
if(n == 0)
return 1;
int x;
long long ans;
x = improvement_pow_mod(a, n/2, m); //每次规模减少一半
ans = (long long)x * x % m;
if(n % 2)
ans = ans * a % m;
return (int)ans;
}
例如:a^29 = (a^14)^2 *a,而a^14 = (a^7)^2, a^7=(a^3)^2*a, a^3=a^2*a,一共只做了7次乘法。不知读者有没有发现,上述递归方式和二分查找很类似-每次规模近似减少一半。因此,时间复杂度为O(logn),比O(n)好了很多(只有1秒多的耗时)。
模线性方程组:
输入正整数a,b,n,解方程ax≡b(mod n)。a,b,n<=10^9
本题中出现了一个新记号:同余。a≡b(modn)的含义是:a和b关于模n同余,即a mod n = b mod n。不难得出,a≡(b mod n)的充要条件是a-b是n的整数倍。
这样,原来的方程就可以理解成 ax-b是n的整数倍。设这个倍数为y,则ax-b=ny,移项得 ax-ny=b,这恰好就是 数论-扩展欧几里得算法 中介绍的不定方程(a,n,b是已知量,x和y是未知数)!接下来的步骤不再介绍。
唯一需要说明的是,如果x是方程的解,满足x≡y(mod n)的其他整数y也是方程的解。因此当谈到同余方程的一个解时,其实指的是一个同余等价类。
有一种特殊情况需要引起读者的重视。b=1时,ax≡1(mod n)的解称为a关于模n的逆,它类似于实数运算中倒数的概念。什么时候a的逆存在呢?根据上面的讨论,方程ax-ny=1要有解。这样,1必须是gcd(a,n)的倍数,因此a和n必须互素(即gcd(a,n)=1),在满足这个条件的前提下,ax≡1(mod n)只有唯一解。注意,同余方程的解是一个等价类。