1. 函数 x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False) ①x: 表示矩阵（也可以是一维） ②ord：范数类型 向量的范数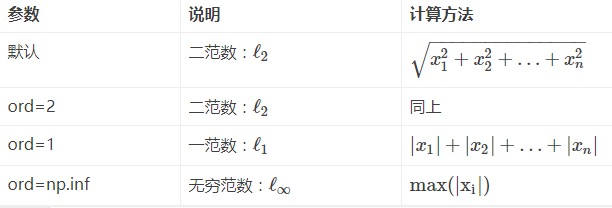： 矩阵的范数： ord=1：列和的最大值 ord=2：|λE-ATA|=0，求特征值，然后求最大特征值得算术平方根 ord=∞：行和的最大值 ③axis：处理类型 axis=1表示按行向量处理，求多个行向量的范数 axis=0表示按列向量处理，求多个列向量的范数 axis=None表示矩阵范数。 ④keepding：是否保持矩阵的二维特性 True表示保持矩阵的二维特性，False相反     代码如下： # 求向量的三种范式
A = np.array([[3,4],[-6,5]]) ret = np.linalg.norm(A,ord=None) # 对象是矩阵，求矩阵元素平方和开放
print(ret)
# In[34]
ret = np.linalg.norm(A,ord=None,axis=1) # 对象是逐行，求每行元素平方和开放
print(ret)
# In[35]
ret = np.linalg.norm(A,ord=None,axis=0)  # 对象是逐列，求每列元素平方和开放
print(ret)
# In[36]
# 对象是矩阵，求矩阵中逐行元素绝对值和的最大值
ret = np.linalg.norm(A,ord=np.Inf)
print(ret)
# In[37]
ret = np.linalg.norm(A,ord=np.Inf,axis=1) # 对象是逐行，求每行元素绝对值和的最大值
print(ret)
# In[38]
ret = np.linalg.norm(A,ord=np.Inf,axis=0) # 对象是逐列，求每列元素绝对值的最大值
print(ret)
# In[39]
# 对象是矩阵，求矩阵中逐行元素绝对值和的最小值
ret = np.linalg.norm(A,ord=-np.Inf)  
print(ret) ret = np.linalg.norm(A,ord=-np.Inf,axis=1) # 对象是逐行，求行的元素绝对值的最小值
print(ret) ret = np.linalg.norm(A,ord=-np.Inf,axis=0) # 对象是逐列，求列的元素绝对值的最小值
print(ret)
# In[40]
A = np.array([[3,-4,1],[-6,5,0]]) ret = np.linalg.norm(A,ord=0,axis=1) # 对象是逐行，求每行的非零元素个数
print(ret)
# In[41]
ret = np.linalg.norm(A,ord=0,axis=0) # 对象是逐列，求每列的非零元素个数
print(ret)
# In[42]
A = np.array([[100,4],[-6,5]])
ret = np.linalg.norm(A,ord=1)   # 对象是矩阵，求列的元素绝对值和的最大值
print(ret) ret = np.linalg.norm(A,ord=1,axis=1)  # 对象是逐行，求行的元素绝对值和
print(ret) ret = np.linalg.norm(A,ord=1,axis=0)    # 对象是逐列，求；列的元素绝对值和
print(ret)
# In[43]    
A = np.array([[-4,3,1],[-6,5,-1]])
ret = np.linalg.norm(A,ord=-1)  # 对象是矩阵，求列的元素绝对值和最小值
print(ret)
ret = np.linalg.norm(A,ord=-1,axis=1) # 对象是逐行
print(ret)
ret = np.linalg.norm(A,ord=-1,axis=0)  # 对象是逐列
print(ret)
# In[44]
A = np.array([[-4,  3, 4],
                  [-6,  4, 3]])
#10.0015300174, 对象是矩阵，求所有元素平方和开方，所有元素平方和102，开方=10.0015300174
ret = np.linalg.norm(A, ord=2)
#[ 6.40312424  7.81024968]，对象是每行，求行的元素平方和开方
ret = np.linalg.norm(A, ord=2, axis=1)
#[ 7.21110255  5. 5.]，对象是每列，求列的元素平方和开方
ret = np.linalg.norm(A, ord=2, axis=0)