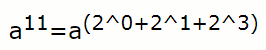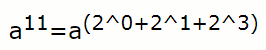快速幂原文        快速幂这个东西比较好理解，但实现起来到不老好办，记了几次老是忘，今天把它系统的总结一下防止忘记。 　　首先，快速幂的目的就是做到快速求幂，假设我们要求a^b,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(b)也即是O(n)级别，快速幂能做到O(logn)，快了好多好多。它的原理如下： 　　假设我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，例如当b==11时 　　　　　　　　　　　　　　　　　　　　　 　　11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算 a2^0*a2^1*a2^3，也就是a1*a2*a8 ，看出来快的多了吧原来算11次，现在算三次，但是这三项貌似不好求的样子....不急，下面会有详细解释。                                                   由于是二进制，很自然地想到用位运算这个强大的工具：&和>>，&运算通常用于二进制取位操作，例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶，x&1==1为奇。>>运算比较单纯,二进制去掉最后一位，不多说了，先放代码再解释。   int Pow(int a, int b) { int ans = 1; while (b) { if (b & 1) ans *= a ; a *= a; b >>= 1; } return ans; }   　　代码很短，死记也可行，但最好还是理解一下吧，其实也很好理解，以b==11为例，b=>1011,二进制从右向左算，但乘出来的顺序是 a^(2^0)*a^(2^1)*a^(2^3)，是从左向右的。我们不断的让base*=base目的即是累乘，以便随时对ans做出贡献。 　　其中要理解base*=base这一步：因为 base*base==base2，下一步再乘，就是base2*base2==base4，然后同理  base4*base4=base8，由此可以做到base-->base2-->base4-->base8-->base16-->base32.......指数正是 2^i ，再看上面的例子，a¹¹= a1*a2*a8，这三项就可以完美解决了，快速幂就是这样。   快速幂取模运算原理：ab mod c=(a mod c)(b mod c)mod c ；   代码： int PowMod(int a, int b, int c) { int ans = 1; a %= c; while (b) { if (b & 1) ans = (ans * a) % c; a = (a * a) % c; b >>= 1; } return ans; }