题目：

答案：

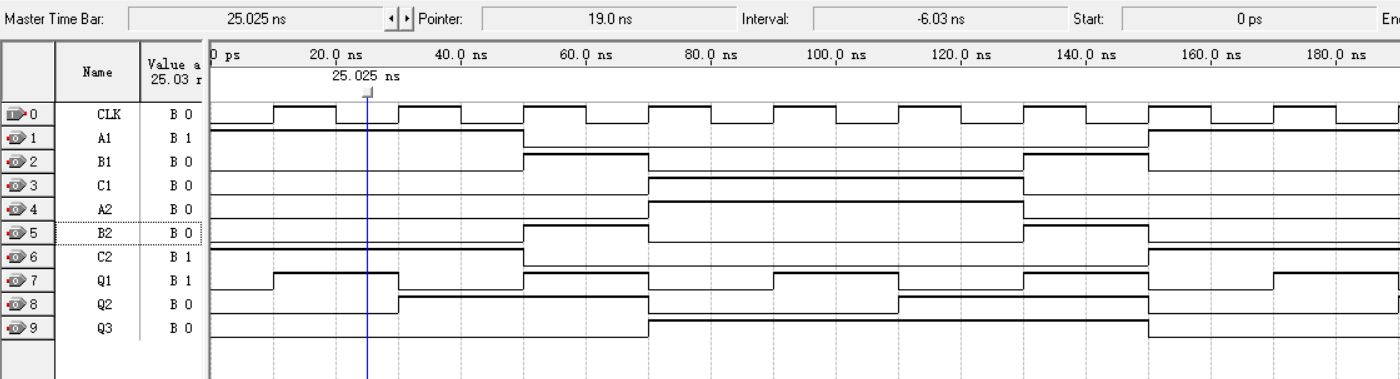
工程文件下载：https://github.com/BlademasterQAQ/A-simple-traffic-signal-lamp-in-digital-electronic-technology   用3个JK触发器实现的3位二进制计数器电路：   仿真结果：（此为上升沿触发时的仿真结果，改为下降沿触发才正常（向右平移半个CLK））   思考题：如何将时间增大10倍？（红灯3s变30s） 由于实验箱提供1Hz的方波信号，1个CLK周期正好是1s，所以一个高电平持续多少个CLK周期就说明了持续多少秒。 若时间增大10倍，很容易想到CLK周期变成10s就行，即输入0.1Hz的方波信号，但这在实验箱是不可行的，我们只能用电路来实现。 我们知道触发器对上升沿/下降沿有效，那么只要将10s内的10个方波信号变成1个就行（忽略前9个方波，最后一个产生一个方波）。 在数学中，这便是逢十进一——十进制的原理，第10个方波才产生进位（1个方波）。 用74160的CO输出端就能简单实现了（每10个CLK，CO输出一个方波）     （p.s:非常感谢学长提供的答案给我带来的帮助   https://blog.csdn.net/iRay007/article/details/6945968） 只需要答案的同学们可以离开了o(*￣▽￣*)o  

---

解析：

题目要求用3个JK触发器和6个与非门实现电路， 而提示中将电路分为了两部分： 1.将CLK时钟信号转换为3位二进制数据的计数器 2.通过逻辑函数用3位二进制数据控制电路   其中的第2点在前面几章中我们就已经会将二进制数据通过真值表写出逻辑函数、化简，便可得控制电路，这里不做赘述。 而第1点将CLK时钟信号转换为3位二进制数据需用到第五章新学的触发器。  

如何将CLK时钟信号通过触发器转换为二进制数据？

触发器原理： 首先我们知道触发器的功能是在CLK和输入信号的作用下能实现输出信号高低电平的转换 对于SR主从触发器，当CLK=1时，S=R=0时保持原输出，S=1，R=0时置1，S=0，R=1时置0 而JK触发器比其他触发器特殊在J=K=1时为原输出的反转（Q*=Q‘） JK触发器的状态方程：Q*=JQ’+K‘Q   二进制计数器原理： 二进制计数器实际就为加法器，只是在触发器中变成每产生一个CLK=1的上升沿时，让二进制数据加1  

• 推测法：

（笔者未学时序电路分析时的用的方法） Q1是最低位，每一个CLK=1到来时就应该反转一次，这正对应前面所说的 “ J=K=1时为原输出的反转 ” 。 所以输出Q1的触发器J、K都接Vcc即可。   Q2是第二位，当Q1是0时，下个CLK=1时Q1变1，无进位，Q2不变；当Q1是1时，下个CLK时Q1产生进位，Q2=原Q2+1 再考虑原Q2为0或1的情况，有以下真值表： Q1 Q2 Q2* 0 0 0 0 1 1 1 0 1 1 1 0                           Q2*为下一个CLK=1时的Q2的值   上表为二进制简单的进位关系，转化为逻辑方程得：Q2*=Q1Q2’+Q1‘Q2 对应JK触发器的状态方程可知输出Q2的触发器只要满足输入J=Q1，K’=Q1‘（即K=Q1）即可实现该真值表 所以第二个JK触发器的输入端J、K连接第一个JK触发器的输出   Q3同理，用二进制进位写出真值表： Q1 Q2 Q3 Q3* 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0                                                                                    Q3*为下一个CLK=1时的Q3的值   转化为逻辑方程并化简得：Q3*=(Q1Q2)'Q3+(Q1Q2)Q3' 对应状态方程可知第三个JK触发器的输入应为J=K=Q1Q2 由题目要求限制，需用两个与非门（其中一个当非门使用）实现。 这样，这题的难点就被攻克了(●ˇ∀ˇ●)  

• 标准方法：

更简便的方法应该用状态转换表和次态卡诺图求解（当时笔者还未学习到） 3位二进制计数器状态转换表（循环）： CLK Q3 Q2 Q1 Q3* Q2* Q1* 0 0 0 0 0 0 1 1 0 0 1 0 1 0 2 0 1 0 0 1 1 3 0 1 1 1 0 0 4 1 0 0 1 0 1 5 1 0 1 1 1 0 6 1 1 0 1 1 1 7 1 1 1 0 0 0                     （取初始状态Q3 Q2 Q1 = 0 0 0） （上一个时钟信号的Q3* Q2* Q1*作为下一次时钟信号的Q3 Q2 Q1输入） 这样每个时钟信号的次态和原状态间构成的简单的二进制加法关系 写出Q3* Q2* Q1*关于Q3 Q2 Q1的逻辑方程，再对应JK触发器的特性方程，即可得电路的逻辑结构图。   （注意：Quartus中的JK触发器名为jkff,为上升沿触发（与课本示例不同），若要使第一个灯是3s而不是2.5s，应在JK触发器前加一个非门，使之变成下降沿触发的JK触发器）