本文的思想来自wikipedia
所谓模幂,就是计算(b^e) mod m的值。这里b、e、m都为给定的某个值。
比如计算(5^3) mod 13 或者计算 (4^13) mod 497。 这里介绍三种计算模幂的方法:效率当然是越来越高效。
1. c mod m = (a ⋅ b) mod m
2. c mod m = [(a mod m) ⋅ (b mod m)] mod m
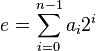
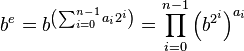
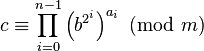
程序如下:
比如计算(5^3) mod 13 或者计算 (4^13) mod 497。 这里介绍三种计算模幂的方法:效率当然是越来越高效。
1.直接计算方法
根本不用思考先算 ,直接先计算b^e, 然后再mod m。2 Memory-efficient method**
两个基本的等式:1. c mod m = (a ⋅ b) mod m
2. c mod m = [(a mod m) ⋅ (b mod m)] mod m
The algorithm is as follows:
Set c = 1, e′ = 0.
Increase e′ by 1.
Set c = (b ⋅ c) mod m.
If e′ < e, goto step 2. Else, c contains the correct solution to c ≡ be mod 'm.
其实就是乘一次模一次;比如按这种方法计算 (4^13) mod 497的过程如下:
e' = 1. c = (1 * 4) mod 497 = 4 mod 497 = 4.
e' = 2. c = (4 * 4) mod 497 = 16 mod 497 = 16.
e' = 3. c = (16 * 4) mod 497 = 64 mod 497 = 64.
e' = 4. c = (64 * 4) mod 497 = 256 mod 497 = 256.
e' = 5. c = (256 * 4) mod 497 = 1024 mod 497 = 30.
e' = 6. c = (30 * 4) mod 497 = 120 mod 497 = 120.
e' = 7. c = (120 * 4) mod 497 = 480 mod 497 = 480.
e' = 8. c = (480 * 4) mod 497 = 1920 mod 497 = 429.
e' = 9. c = (429 * 4) mod 497 = 1716 mod 497 = 225.
e' = 10. c = (225 * 4) mod 497 = 900 mod 497 = 403.
e' = 11. c = (403 * 4) mod 497 = 1612 mod 497 = 121.
e' = 12. c = (121 * 4) mod 497 = 484 mod 497 = 484.
e' = 13. c = (484 * 4) mod 497 = 1936 mod 497 = 445.
伪代码如下:
function modular_pow(base, exponent, modulus)
if modulus = 1 then return 0
c := 1
for e_prime = 1 to exponent
c := (c * base) mod modulus
return c
3.Right-to-left binary method
将幂写出二进制形式。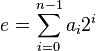
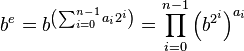
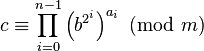
程序如下:
int modpow(int base, int exponent, int modulus) {
int result = 1;
while (exponent > 0) {
if (exponent & 1) {
// multiply in this bit's contribution while using modulus to keep result small
result = (result * base) % modulus;
}
// move to the next bit of the exponent, square (and mod) the base accordingly
exponent >>= 1;
base = (base * base) % modulus;
}
return result;
}
int main()
{
cout << modpow(4, 13, 497) << endl;
}