用A1 B1 C1 D1 对M1,M2,M3,M4 加密
  A2 B2 C2 D2
  A3 B3 C3 D3
算法
  (M1 xor A3 xor  0)*A2 mod A1=N1  N1 and FFFF=S1
  (M2 xor B3 xor S1)*B2 mod B1=N2  N2 and FFFF=S2
  (M3 xor C3 xor S2)*C2 mod C1=N3  N3 and FFFF=S3
  (M4 xor D3 xor S3)*D3 mod D1=N4  N4 and FFFF=S4

最后生成的明文为N1,N2,N3,N4

现在已知N1,N2,N3,N4, A1,B1,....C3,D3
知道M1,M2,M3,M4为WORD类型,其他的为整数类型

问应该怎么对N1,N2,N3,N4进行解密操作

现在我的考虑是这个数据不能直接的解密,可能解密还应
该有一个解密的密码表,但是解密的密码表应该可以用加
密的密码表算出来,不知道我说的对不对,各位大侠帮小
弟看看,谢谢了，

关于一个解密算法的解答

作者  ：  zmworm
E-Mail:  zmworm@sohu.com
HomePage: ZMWorm.Yeah.Net



blueboy问如下问题：

用A1 B1 C1 D1 对M1,M2,M3,M4 加密
  A2 B2 C2 D2
  A3 B3 C3 D3
算法
  (M1 xor A3 xor  0)*A2 mod A1=N1  N1 and FFFF=S1
  (M2 xor B3 xor S1)*B2 mod B1=N2  N2 and FFFF=S2
  (M3 xor C3 xor S2)*C2 mod C1=N3  N3 and FFFF=S3
  (M4 xor D3 xor S3)*D2 mod D1=N4  N4 and FFFF=S4

最后生成的明文为N1,N2,N3,N4

现在已知N1,N2,N3,N4, A1,B1,....C3,D3
知道M1,M2,M3,M4为WORD类型,其他的为整数类型

问应该怎么对N1,N2,N3,N4进行解密操作

现在我的考虑是这个数据不能直接的解密,可能解密还应
该有一个解密的密码表,但是解密的密码表应该可以用加
密的密码表算出来,不知道我说的对不对,各位大侠帮小
弟看看,谢谢了，

答案如下：

因为是字长是WORD，所以
N1=S1
N2=S2
N3=S3
N4=S4

所以加密变换化简为[a]
(M1 xor A3 xor  0)*A2 mod A1=N1
(M2 xor B3 xor N1)*B2 mod B1=N2
(M3 xor C3 xor N2)*C2 mod C1=N3 
(M4 xor D3 xor N3)*D2 mod D1=N4

设
K1=(M1 xor A3 xor  0)
K2=(M2 xor B3 xor N1)
K3=(M3 xor C3 xor N2)
K4=(M4 xor D3 xor N3)


加密变换化简为[b]
K1*A2 mod A1=N1
K2*B2 mod B1=N2
K3*C2 mod C1=N3 
K4*D3 mod D1=N4

只要我们能求出Ki，Mi也就可求了 因为
M1=(K1 xor A3 xor  0)
M2=(K2 xor B3 xor N1)
M3=(K3 xor C3 xor N2)
M4=(K4 xor D3 xor N3)

所以问题的关键是求 Ki 注意到[b]中每一等式中只有Ki未知，其他量都已知。不妨设

K*e mod f = d (e,f,d为已知量）[c]

设e'为 e 关于f的乘法逆元
（什么是乘法逆元？若e'满足e*e' mod f =1 则称e'为 e 关于f的乘法逆元）
则有
e'*e mod f= 1
根据模运算性质有
d*(e'*e) mod f=d*1=d    [d]

对比 [c] [d] 不难发现
K=d*e' mod f

所以问题转为求e的乘法逆元e'
用扩展的欧几里德算法 可以求e' .算法描述如下
ExtendedEuclid(e,f)
1 （X1,X2,X3):=(1,0,f)
2  (Y1,Y2,Y3):=(0,1,e)
3  if (Y3=0) then return  e'=null//无逆元
4  if (Y3=1) then return  e'=Y2  //Y2为逆元
5  Q:=X3 div Y3
6  (T1,T2,T3):=(X1-Q*Y1,X2-Q*Y2,X3-Q*Y3)
7 （X1,X2,X3):=(Y1,Y2,Y3)
8  (Y1,Y2,Y3):=(T1,T2,T3)
9  goto 3

看不明白算法？我们举个例子：求7关于96的乘法逆元。

 
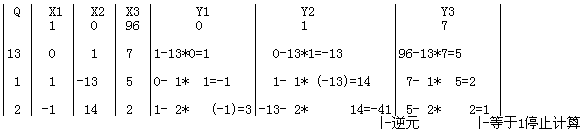
扩展辗转相除法图示


-41 mod 96 =55 所以55就是7关于96的逆元。
让我们检验一下55*7 mod 96 =1

最后我们取求K的例子，K*7 mod 96 = 13 求K
因为7的乘法逆元是55 所以  K=13*55 mod 96=715 mod 96=43  K=43
检验 43*7 mod 96=288 mod 96 =13

总结解密算法:
K1=:A2'*N1 mod A1
K2=:B2'*N2 mod B1
K3=:C2'*N3 mod C1 
K4=:D2'*N4 mod D1

M1=(K1 xor A3 xor  0)
M2=(K2 xor B3 xor N1)
M3=(K3 xor C3 xor N2)
M4=(K4 xor D3 xor N3)

小结：通过这道问题的解答，我们学习到一些新的知识，知道了什么是乘法逆元，乘法逆元在密码学中的作用也重要，RSA算法就用到了乘法逆元，感兴趣的话，你可以参考RSA方面的书籍。祝你学习愉快！！

关于一个解密算法的解答(补充)

作者  :  zmworm
E-Mail:  zmworm@sohu.com
HomePage: ZMWorm.Yeah.Net

    刚才说的情况是 e'存在的情况，若e'不存在，应该怎样解密呢？

    首先，我们要知道e满足什么条件时，e'存在。我们有以下定理：

        如果gcd(e,f)=1(即 e,f 互素)，那么e有一个模f的乘法逆元。
        [gcd(e,f)=p,表示e,f的最大公约数是p,求最大公约数可以用辗转相除法]

    如果gcd(e,f)=p(p>1) 则 不存在e关于f的乘法逆元。


    现在我们就求乘法逆元不存在时 K*e mod f=d 的解-----------------[e]

        因为 gcd(e,f)=p 所以 p|e, p|f,设 e"=e/p ,f"=f/p ,m=K*e div f,则
        K*e mod f=d => K*e=m*f+d => K*e"*p=m*f"*p+d => d=K*e"*p-m*f"*p=(K*e"-m*f")*p

        所以 p|d, 令 d"=d/p ,则
        K*e mod f=d => K*e"*p=m*f"*p+d"*p => K*e"=m*f"+d" => K*e" mod f"=d"

        而 gcd(e",f")=1,这样我们就可以求e"的逆元e'
        所以 d"*(e'*e") mod f"=d" =>d"*e'*e"*p mod f"*p=d"p
        即 (d"*e')*e mod f=d -------------------------------------[f]

        对比[e] [f] 有 K=d"*e'


        注意 这只是K的一个解
        事实上，Ki=d"*e'+(i-1)f"  (i=1..p) 都满足条件, 因为 (d"*e'+if")*e" mod f"=d"

        也就是说，若gcd(e,f)=p 则K有p个值

    [例] 求 满足K*14 mod 96 =12中K的值

    解 因为gcd(14,96)=2,所以k 有两个解
    e"=14/2=7 f"=96/2=48 d"=12/2=6
    7关于 48的逆元e'=7 (因为 7*7 mod 48 =1)
    所以 Ki=d"*e'+(i-1)f"=6*7+（i-1)*48 (i=1,2)
    解得 K1=42 K2=90

若不存在逆元的解密算法为

K1=:A2'*N1" mod A1
K2=:B2'*N2" mod B1
K3=:C2'*N3" mod C1 
K4=:D2'*N4" mod D1

M1=(K1 xor A3 xor  0)
M2=(K2 xor B3 xor N1)
M3=(K3 xor C3 xor N2)
M4=(K4 xor D3 xor N3)

关于一个解密算法的解答(对K的补充说明)

作者  :  zmworm
E-Mail:  zmworm@sohu.com
HomePage: ZMWorm.Yeah.Net


(1)若不存在逆元，求K时
    Ki=d"*e'+(i-1)f"
    若 d"*e' 大于 f"时需要进行模运算 即Ki=[(d"*e') mod f"]+(i-1)f"

(2)前面的方法我们已经可以求出至少一组明文，如果您想求出所有满足条件的解，你还要继续往下看。

    细心的您一定发现了我们前面所求得K都是小于f的，而事实上
    若K满足K*e mod f=d ,则所有的Ki=K+i*f(i=1..n) 也满足Ki*e mod f=d
    那么说满足K*e mod f=d的 K应该有无数多个。

    在数学中的确如此，
    在计算机中则不同，要根据字长设字长为n,对每一个K
    应该有 2^n div f 或(2^n div f)+1个
    只要Ki=K+i*f <2^n 都满足
    Ki=K+i*f >2^n 就会发生溢出错误了。

关于一个解密算法的解答(此算法的具体例子)

作者  :  zmworm
E-Mail:  zmworm@sohu.com
HomePage: ZMWorm.Yeah.Net 

[习题]
以下各变量的字长均为8位

用A1=96  B1=96 C1=97 D1=97 
  A2=7  B2=14 C2=21 D2=28
  A3=33  B3=34 C3=35 D3=36
算法 
  (M1 xor A3 xor  0)*A2 mod A1=N1 
  (M2 xor B3 xor N1)*B2 mod B1=N2 
  (M3 xor C3 xor N2)*C2 mod C1=N3
  (M4 xor D3 xor N3)*D2 mod D1=N4
对M1,M2,M3,M4 进行加密操作

求得
  (M1 xor 33 xor  0)*7  mod 96=86
  (M2 xor 34 xor 86)*14 mod 96=80 
  (M3 xor 35 xor 80)*21 mod 97=93
  (M4 xor 36 xor 93)*28 mod 97=25 
即密文为  N1=86 N2=80 N3=93 N4=25

问所有可能的明文M1 M2 M3 M4

解

gcd(7,96)=1 所以K1 有一个解
7模96的乘法逆元为55 (因为 7*55 mod 96=1)
所以K1=55*N1 mod 96 =26
K1所有可能情况是 26 ,26+96=122 ,122+96=218,
M1=26 xor 33 xor 0=59
M1=122 xor 33 xor 0=91
M1=218 xor 33 xor 0=251

M1 的所有可能是 59, 91, 251


gcd(14,96)=2,所以k 有两个解
e"=14/2=7 f"=96/2=48 d"=80/2=40
7关于 48的逆元e'=7 (因为 7*7 mod 48 =1)
所以 K2[i]i=d"*e'+(i-1)f"=[(40*7) mod 48]+（i-1)*48 (i=1,2)
解得 K2[1]=40 K2[2]=88
K2所有可能情况是 40 ,40+96=136 ,136+96=232, 88 88+96=184
M2=40 xor 34 xor 86=92
M2=136 xor 34 xor 86=252
M2=232 xor 34 xor 86=156
M2=88 xor 34 xor 86=44
M2=184 xor 34 xor 86=204

M2的所有可能是 92, 252, 156, 44, 206

gcd(21,97)=1 所以K1 有一个解
模96的乘法逆元为37 (因为 37*21 mod 97=1)
所以K1=37*N3 mod 97 =46
K1所有可能情况是 46 ,46+97=143 ,143+97=240,
M3=46 xor 35 xor 80=93
M3=143 xor 35 xor 80=252
M3=240 xor 35 xor 80=136

M2的所有可能是 93, 252, 136


M4 留为作业 ，自己求。答案不确定可以问我。