{var%20f='http://v.t.sina.com.cn/share/share.php?appkey=1515056452',u=z||d.location,p=['&url=',e(u),'&title=',e(t||d.title),'&source=',e(r),'&sourceUrl=',e(l),'&content=',c||'gb2312','&pic=',e(p||'')].join('');function%20a(){if(!window.open([f,p].join(''),'mb',['toolbar=0,status=0,resizable=1,width=440,height=430,left=',(s.width-440)/2,',top=',(s.height-430)/2].join('')))u.href=[f,p].join('');};if(/Firefox/.test(navigator.userAgent))setTimeout(a,0);else%20a();})(screen,document,encodeURIComponent,'','','https://www.xiaopingtou.cn//data/attach/topic/topicKPo7gB.jpg', '推荐 elementtang 的文章《除法取模 逆元 费马小定理》','https://www.xiaopingtou.net/article-51567.html','页面编码gb2312|utf-8默认gb2312'));){kind=link}
对于正整数
和
，如果有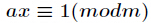
，那么把这个同余方程中
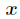的最小正整数解叫做模的逆元。
逆元一般用扩展欧几里得算法来求得，如果为素数，那么还可以根据费马小定理得到逆元为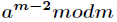
。（都要求a和m互质）
推导过程如下(逆元详解)（点我） 假如p是质数，且gcd(a,p)=1，那么 a(p-1)≡1（mod p）这个为费马小定理，m为素数是费马小定理的前置条件。
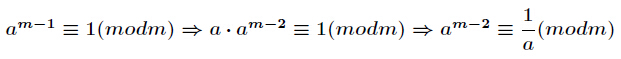求a/b=x(mod
M）
只要M是一个素数,而且b不是M的倍数,就可以用一个逆元整数b1,通过
a/b=a*b1 (mod M)，只能来以乘换除。
费马小定理:对于素数 M 任意不是 M 的倍数的 b，都有：b ^ (M-1) = 1 (mod M)
于是可以拆成：b*b^(M-2)=1(mod M)
于是:a/b=a/b*(b * b ^ (M-2))=a*(b ^ (M-2)) (mod M) 求a/b=x(mod M) 用扩展欧几里德算法算出b1,然后计算a*b1(mod M) exgcd(b,M,x,y); b1=x; 当p是个质数的时候有
inv(a) = (p - p / a) * inv(p % a) % p 证明： 设x = p % a,y = p / a
于是有 x + y * a = p
(x + y * a) % p = 0
移项得 x % p = (-y) * a % p
x * inv(a) % p = (-y) % p
inv(a) = (p - y) * inv(x) % p
于是 inv(a) = (p - p / a) * inv(p % a) % p 然后一直递归到1为止，因为1的逆元就是1。
和，如果有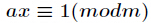，那么把这个同余方程中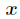的最小正整数解叫做模的逆元。逆元一般用扩展欧几里得算法来求得，如果
为素数，那么还可以根据费马小定理得到逆元为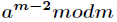。（都要求a和m互质）推导过程如下(逆元详解)（点我） 假如p是质数，且gcd(a,p)=1，那么 a(p-1)≡1（mod p）这个为费马小定理，m为素数是费马小定理的前置条件。
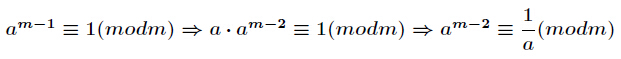求a/b=x(mod
M）
只要M是一个素数,而且b不是M的倍数,就可以用一个逆元整数b1,通过
a/b=a*b1 (mod M)，只能来以乘换除。费马小定理:对于素数 M 任意不是 M 的倍数的 b，都有：b ^ (M-1) = 1 (mod M)
于是可以拆成：b*b^(M-2)=1(mod M)
于是:a/b=a/b*(b * b ^ (M-2))=a*(b ^ (M-2)) (mod M) 求a/b=x(mod M) 用扩展欧几里德算法算出b1,然后计算a*b1(mod M) exgcd(b,M,x,y); b1=x; 当p是个质数的时候有
inv(a) = (p - p / a) * inv(p % a) % p 证明： 设x = p % a,y = p / a
于是有 x + y * a = p
(x + y * a) % p = 0
移项得 x % p = (-y) * a % p
x * inv(a) % p = (-y) % p
inv(a) = (p - y) * inv(x) % p
于是 inv(a) = (p - p / a) * inv(p % a) % p 然后一直递归到1为止，因为1的逆元就是1。
void init() //O(n)求逆元
{
inv[1] = 1;
for(int i = 2;i <= N;i ++)
{
inv[i] = (mod - mod/i) * inv[mod % i] % mod;
}
// for(int i=1; i<=10;i++)
//cout</*
总结：求逆元的方法
在 mod 的情况下，(a*b/c)%mod不能直接/c来求，需要找到一个数inv使得 inv*c % mod =1.这样(a*b/c)%mod = (a*b*inv)%mod
性质：逆元是积性函数，存在a*b=c,那么 inv[c]=inv[a] * inv[c] %mod
1, 暴力循环找解
2，费马小定理的解法：mod是质数才能用
3，利用欧几里得扩展来求。
欧几里得扩展是用来解决 ax +by=gcd(a,b)这样的式子
这时候取 b=mod，你可以写成这样，ax=gcd(a,b)-by
推导出 a*x % mod=gcd(a,b)%mod
所以只要gcd(a,b)%mod==1是就可以使用这种方法来求逆元
4，利用神奇的推导，O(n) 求出 1~n的所有逆元(参考上面的 init())
5, 利用逆元函数是完全积性函数的性质,O(logN)求单个数的逆元
*/
它可以在O(n)的复杂度内算出n个数的逆元。
#include
const int N = 200000 + 5;
const int MOD = (int)1e9 + 7;
int inv[N];
int init()
{
inv[1] = 1;
for(int i = 2; i < N; i ++)
inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
}
int main()
{
init();
}