定义:设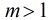 ,
,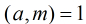 ,使得
,使得 成立的最小的
成立的最小的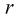 ,称为
,称为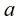 对模
对模 的阶,记为
的阶,记为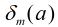 。
。
定理:如果模 有原根,那么它一共有
有原根,那么它一共有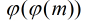 个原根。
个原根。
定理:若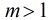 ,
,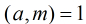 ,
,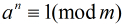 ,则
,则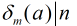 。
。
定理:如果 为素数,那么素数
为素数,那么素数 一定存在原根,并且模
一定存在原根,并且模 的原根的个数为
的原根的个数为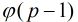 。
。
定理:设 是正整数,
是正整数, 是整数,若
是整数,若 模
模 的阶等于
的阶等于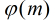 ,则称
,则称 为模
为模 的一个原根。
的一个原根。
假设一个数 对于模
对于模 来说是原根,那么
来说是原根,那么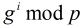 的结果两两不同,且有
的结果两两不同,且有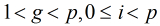 ,那么
,那么 可以称为是模
可以称为是模 的一个原根,归根到底就是
的一个原根,归根到底就是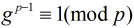 当且仅当指数为
当且仅当指数为 的时候成立。(这里
的时候成立。(这里 是素数)
是素数)
模 有原根的充要条件:
有原根的充要条件: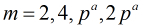 ,其中
,其中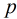 是奇素数。
是奇素数。
求模素数 原根的方法:对
原根的方法:对 素因子分解,即
素因子分解,即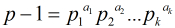 是
是 的标准分解式,若恒有
的标准分解式,若恒有
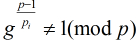
成立,则 就是
就是 的原根。(对于合数求原根,只需把
的原根。(对于合数求原根,只需把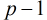 换成
换成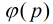 即可)
即可)
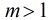 ,
,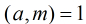 ,使得
,使得 成立的最小的
成立的最小的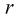 ,称为
,称为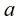 对模
对模 的阶,记为
的阶,记为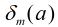 。
。
定理:如果模
 有原根,那么它一共有
有原根,那么它一共有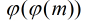 个原根。
个原根。
定理:若
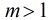 ,
,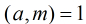 ,
,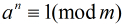 ,则
,则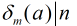 。
。
定理:如果
 为素数,那么素数
为素数,那么素数 一定存在原根,并且模
一定存在原根,并且模 的原根的个数为
的原根的个数为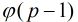 。
。
定理:设
 是正整数,
是正整数, 是整数,若
是整数,若 模
模 的阶等于
的阶等于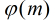 ,则称
,则称 为模
为模 的一个原根。
的一个原根。
假设一个数
 对于模
对于模 来说是原根,那么
来说是原根,那么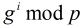 的结果两两不同,且有
的结果两两不同,且有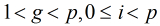 ,那么
,那么 可以称为是模
可以称为是模 的一个原根,归根到底就是
的一个原根,归根到底就是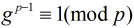 当且仅当指数为
当且仅当指数为 的时候成立。(这里
的时候成立。(这里 是素数)
是素数)
模
 有原根的充要条件:
有原根的充要条件: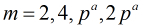 ,其中
,其中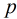 是奇素数。
是奇素数。
求模素数
 原根的方法:对
原根的方法:对 素因子分解,即
素因子分解,即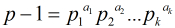 是
是 的标准分解式,若恒有
的标准分解式,若恒有
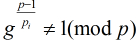
成立,则
 就是
就是 的原根。(对于合数求原根,只需把
的原根。(对于合数求原根,只需把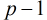 换成
换成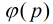 即可)
即可)
#include
#include
#include
#include
#include
#include
#include
using namespace std;
long long d[1000];
long long dp[1000];
int kuai(long long x,long long n,long long m)
{
long long i,j;
long long s=1;
for(i=0;;i++)
{
long long t=x;
long long d=n%2;n=n/2;
if(d==0) t=1;
if(d!=0)
{
if(i==0) t=t*1%m;
else
{
for(j=0;j>p)
{
long long k=p-1;
long long i;
long long x=1;
d[0]=k;
d[1]=1;
if(k%2==0)
{
d[2]=2;
while(k%2==0) k=k/2;
}
long long l=3;
for(long long j=3;j<=k;j+=2)
{
if(k%j==0)
{
d[l]=j;l++;
while(k%j==0) k=k/j;
//cout<