题目大意:
给定两个正整数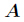 和
和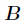 ,求
,求 的所有因子和对9901取余后的值。
的所有因子和对9901取余后的值。
分析: 很容易知道,先把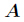 分解得到
分解得到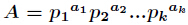 ,那么得到
,那么得到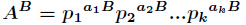 ,那么
,那么 的所有因子和的表达式如下
的所有因子和的表达式如下
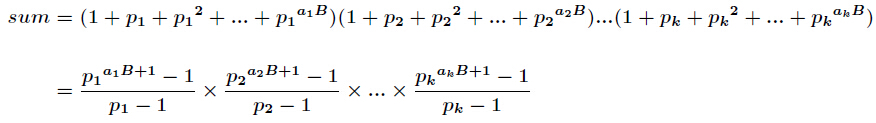 因为要取模且存在除法,所以要用到逆元。
因为要取模且存在除法,所以要用到逆元。
对于正整数 和
和 ,如果有
,如果有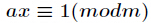 ,那么把这个同余方程中
,那么把这个同余方程中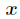 的最小正整数解叫做
的最小正整数解叫做 模
模 的逆元。
逆元一般用扩展欧几里得算法来求得,如果
的逆元。
逆元一般用扩展欧几里得算法来求得,如果 为素数,那么还可以根据费马小定理得到逆元为
为素数,那么还可以根据费马小定理得到逆元为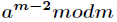 。
推导过程如下
。
推导过程如下
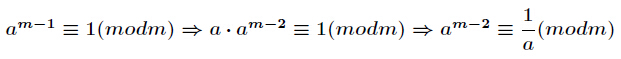 求现在来看一个逆元最常见问题,求如下表达式的值(已知
求现在来看一个逆元最常见问题,求如下表达式的值(已知 )
)
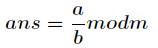 当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果 是素数,还可以用费马小定理。
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求
是素数,还可以用费马小定理。
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求 与
与 互素。实际上我们还有一
种通用的求逆元方法,适合所有情况。公式如下
互素。实际上我们还有一
种通用的求逆元方法,适合所有情况。公式如下
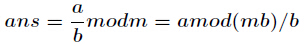 现在我们来证明它,已知
现在我们来证明它,已知 ,证明步骤如下
,证明步骤如下
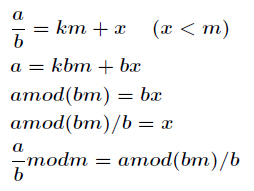
等比数列求和公式,用如下公式即可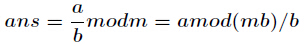 因为
因为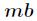 可能会很大,超过int范围,所以在快速幂时要二分乘法。
可能会很大,超过int范围,所以在快速幂时要二分乘法。
接下来就是代码了:(一定要讲乘法二分,还有取模后一定要加模)
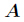 和
和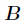 ,求
,求 的所有因子和对9901取余后的值。
的所有因子和对9901取余后的值。分析: 很容易知道,先把
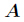 分解得到
分解得到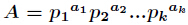 ,那么得到
,那么得到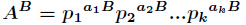 ,那么
,那么 的所有因子和的表达式如下
的所有因子和的表达式如下
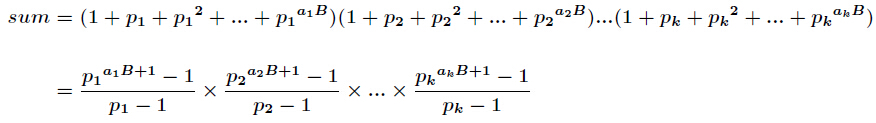 因为要取模且存在除法,所以要用到逆元。
因为要取模且存在除法,所以要用到逆元。
对于正整数
 和
和 ,如果有
,如果有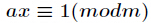 ,那么把这个同余方程中
,那么把这个同余方程中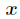 的最小正整数解叫做
的最小正整数解叫做 模
模 的逆元。
逆元一般用扩展欧几里得算法来求得,如果
的逆元。
逆元一般用扩展欧几里得算法来求得,如果 为素数,那么还可以根据费马小定理得到逆元为
为素数,那么还可以根据费马小定理得到逆元为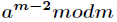 。
推导过程如下
。
推导过程如下
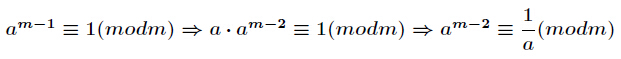 求现在来看一个逆元最常见问题,求如下表达式的值(已知
求现在来看一个逆元最常见问题,求如下表达式的值(已知 )
)
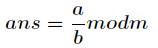 当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果 是素数,还可以用费马小定理。
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求
是素数,还可以用费马小定理。
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求 与
与 互素。实际上我们还有一
种通用的求逆元方法,适合所有情况。公式如下
互素。实际上我们还有一
种通用的求逆元方法,适合所有情况。公式如下
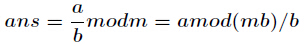 现在我们来证明它,已知
现在我们来证明它,已知 ,证明步骤如下
,证明步骤如下
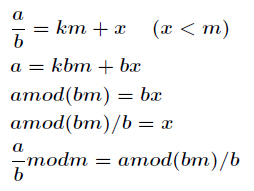
等比数列求和公式,用如下公式即可
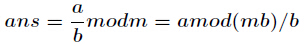 因为
因为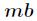 可能会很大,超过int范围,所以在快速幂时要二分乘法。
可能会很大,超过int范围,所以在快速幂时要二分乘法。
接下来就是代码了:(一定要讲乘法二分,还有取模后一定要加模)
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include