在51nod上看到一道原根的题,结果一脸懵比,,赶紧找了一篇资料,,,
定义:设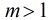 ,
,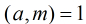 ,使得
,使得 成立的最小的
成立的最小的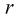 ,称为
,称为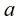 对模
对模 的阶,记为
的阶,记为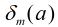 。
。
定理:如果模 有原根,那么它一共有
有原根,那么它一共有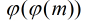 个原根。
个原根。
定理:若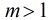 ,
,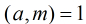 ,
,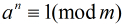 ,则
,则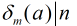 。
。
定理:如果 为素数,那么素数
为素数,那么素数 一定存在原根,并且模
一定存在原根,并且模 的原根的个数为
的原根的个数为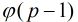 。
。
定理:设 是正整数,
是正整数, 是整数,若
是整数,若 模
模 的阶等于
的阶等于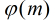 ,则称
,则称 为模
为模 的一个原根。
的一个原根。
假设一个数 对于模
对于模 来说是原根,那么
来说是原根,那么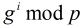 的结果两两不同,且有
的结果两两不同,且有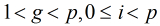 ,那么
,那么 可以称为是模
可以称为是模 的一个原根,归根到底就是
的一个原根,归根到底就是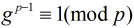 当且仅当指数为
当且仅当指数为 的时候成立。(这里
的时候成立。(这里 是素数)
是素数)
模 有原根的充要条件:
有原根的充要条件: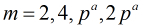 ,其中
,其中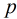 是奇素数。
是奇素数。
求模素数 原根的方法:对
原根的方法:对 素因子分解,即
素因子分解,即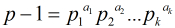 是
是 的标准分解式,若恒有
的标准分解式,若恒有
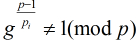
成立,则 就是
就是 的原根。(对于合数求原根,只需把
的原根。(对于合数求原根,只需把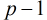 换成
换成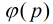 即可)
即可)
[cpp] view plain copy

定义:设
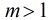 ,
,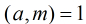 ,使得
,使得 成立的最小的
成立的最小的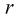 ,称为
,称为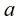 对模
对模 的阶,记为
的阶,记为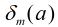 。
。
定理:如果模
 有原根,那么它一共有
有原根,那么它一共有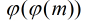 个原根。
个原根。
定理:若
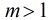 ,
,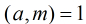 ,
,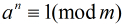 ,则
,则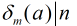 。
。
定理:如果
 为素数,那么素数
为素数,那么素数 一定存在原根,并且模
一定存在原根,并且模 的原根的个数为
的原根的个数为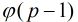 。
。
定理:设
 是正整数,
是正整数, 是整数,若
是整数,若 模
模 的阶等于
的阶等于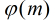 ,则称
,则称 为模
为模 的一个原根。
的一个原根。
假设一个数
 对于模
对于模 来说是原根,那么
来说是原根,那么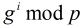 的结果两两不同,且有
的结果两两不同,且有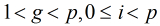 ,那么
,那么 可以称为是模
可以称为是模 的一个原根,归根到底就是
的一个原根,归根到底就是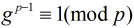 当且仅当指数为
当且仅当指数为 的时候成立。(这里
的时候成立。(这里 是素数)
是素数)
模
 有原根的充要条件:
有原根的充要条件: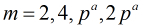 ,其中
,其中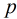 是奇素数。
是奇素数。
求模素数
 原根的方法:对
原根的方法:对 素因子分解,即
素因子分解,即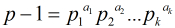 是
是 的标准分解式,若恒有
的标准分解式,若恒有
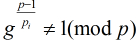
成立,则
 就是
就是 的原根。(对于合数求原根,只需把
的原根。(对于合数求原根,只需把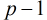 换成
换成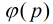 即可)
即可)
[cpp] view plain copy
- #include
- #include
- #include
- #include
- #include
- #include
- using namespace std;
- typedef long long LL;
- const int N = 1000010;
- bitset
prime; - int p[N],pri[N];
- int k,cnt;
- void isprime()
- {
- prime.set();
- for(int i=2; i
- {
- if(prime[i])
- {
- p[k++] = i;
- for(int j=i+i; j
- prime[j] = false;
- }
- }
- }
- void Divide(int n)
- {
- cnt = 0;
- int t = (int)sqrt(1.0*n);
- for(int i=0; p[i]<=t; i++)
- {
- if(n%p[i]==0)
- {
- pri[cnt++] = p[i];
- while(n%p[i]==0) n /= p[i];
- }
- }
- if(n > 1)
- pri[cnt++] = n;
- }
- LL quick_mod(LL a,LL b,LL m)
- {
- LL ans = 1;
- a %= m;
- while(b)
- {
- if(b&1)
- {
- ans = ans * a % m;
- b--;
- }
- b >>= 1;
- a = a * a % m;
- }
- return ans;
- }
- int main()
- {
- int P;
- isprime();
- while(cin>>P)
- {
- Divide(P-1);
- for(int g=2; g
- {
- bool flag = true;
- for(int i=0; i
- {
- int t = (P - 1) / pri[i];
- if(quick_mod(g,t,P) == 1)
- {
- flag = false;
- break;
- }
- }
- if(flag)
- {
- int root = g;
- cout<
- }
- }
- }
- return 0;
- }