为什么求模运算要用素数（质数）—— 哈希表设计

　　在设计用除法来散射的哈希表时，我们都会用数值模哈希表大小，得到的余数来作为ID存入哈希表对应格子中。所有文章都表明要用一个较大的素数来作为哈希表的大小，也就是要模一个较大的素数。但为什么就是要用素数呢？简单分析一下可以看出玄机。 　　先看看如果用一个合数8作为哈希表大小，0-30在哈希表中的散射情况： （表1）

　　再来看看用质数7作为哈希表大小，0-30在哈希表中的散射情况： （表2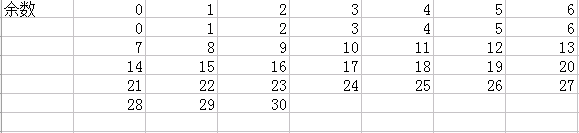） 　　我们都知道，合数8除了1和自身以外，还有2跟4这两个因数。观察表1的单独一列可以发现，这些在同一列的数，他们实际上就是上一个数+8，而查看2、4、6这三行我们发现，因为2 4 6 能被2（或4）整除，而在同一列上的数在+8以后一样满足可以被2（或4）整除的这一特性。例如4这一列，4、12、20、28，这些哈希映射在同一个格子里的数都是前一个数+8，然后他们都能被2和4整除，这样就导致他们之间有很强烈的关系，很容易发生哈希冲突。 　　再来看看表2，同样情况，同一列中的数都是由上一个数+7得到的，但因为7是一个素数，它除了1跟本身之外没有其他因数，所以在同一列的数里就找不到我们刚刚所说的那种特性。 　　而我们都知道，哈希表设计目的就是希望尽量的随机散射，不希望这些在同一列上的元素（也就是会冲突的元素）之间具有关系，所以我们都采用素数作为哈希表的大小，从而避免模数相同的数之间具备公共因数。