• 取模的公式与性质
• 大整数取模
• 幂取模
  • O(n)
  • O(longn)
• 模线性方程组

取模的公式与性质

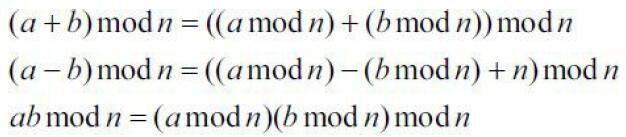
注意在减法中，由于a mod n可能小于b mod n，需要在结果加上n，而在乘法中，需要注
意a mod n和b mod n相乘是否会溢出。例如，当n=109时，ab mod n一定在int范围内，但a mod
n和b mod n的乘积可能会超过int。需要用long long保存中间结果。
如果n本身超过int但又在long long范围内，上述方法就不适用了。在这种情况下，建议使用高精度乘法

大整数取模

把大整数写成“自左向右”的形式：1234=((1*10+2)*10+3)*10+4，然后用前面的公
式，每步取模。 /* ZhangBinjie@Penguin */ #include #include #include #include using namespace std; int main(){ string a; int b, ans = 0; while(cin >> a >> b){ ans = 0; for(int i=0;iint)((long long)ans * 10 + a[i] - 48)% b; } cout << ans << endl; } return 0; }

幂取模

O(n)

/* ZhangBinjie@Penguin //幂取模 O(n) */ #include #include #include using namespace std; int pow_mod(const int &a,const int &n,const int &m){ int ans = 1; for(int i = 0;i < n;++i){ ans = (int)((long long)ans * a % m); } return ans; } int main(){ int a, n, m; while(cin >> a >> n >> m){ cout<< pow_mod(a,n,m)<return 0; }

O(longn)

/* ZhangBinjie@Penguin //幂取模 O(longn) //还能再用记忆化优化 吧？ */ #include #include #include using namespace std; int pow_mod(const int &a,const int &n,const int &m){ if(n == 0) return 1; int x = pow_mod (a,n/2,m); long long ans = (long long)x * x % m; if(n % 2 == 1) ans = ans * a % m; return (int)ans; } int main(){ int a, n, m; while(cin >> a >> n >> m){ cout<< pow_mod(a,n,m)<return 0; }

模线性方程组

输入a, b, n 求解ax≡b(mod n)
显然 ax-b = ny (n为整数）
移项得到 ax-ny = b (n为整数）
这就变成了拓展欧几里得求直线上的点
另外：这样求的的x实际上时同余等价类，即 x≡y(mod n)
具体求解见我的上一篇文章