本文为数字信号处理的学习记录。
一、DSP简介
数字信号处理的过程:模拟信号通过采样/保持电路(S/H)和模电转换电路(A/D),数字化为数字信号x[n],经过DSP处理为新的数字信号y[n],这样的数字信号需要通过D/A转换和低通滤波器(LPF),可以还原为模拟信号作为输出。
 DSP(数字信号处理)相对于ASP(模拟信号处理)的优点:(1)DSP对噪声和温度比较不敏感;(2)DSP具有更高的精度;(3)DSP更容易集成
DSP(数字信号处理)相对于ASP(模拟信号处理)的局限性:A/D D/A转换速率在某些场景下无法达到使用要求。
二、MATLAB基础及其在DSP中的应用
(1)MATLAB基础
在MATLAB中,数组、矩阵与向量在创建和显示的时候没有任何区别、
向量的创建:
DSP(数字信号处理)相对于ASP(模拟信号处理)的优点:(1)DSP对噪声和温度比较不敏感;(2)DSP具有更高的精度;(3)DSP更容易集成
DSP(数字信号处理)相对于ASP(模拟信号处理)的局限性:A/D D/A转换速率在某些场景下无法达到使用要求。
二、MATLAB基础及其在DSP中的应用
(1)MATLAB基础
在MATLAB中,数组、矩阵与向量在创建和显示的时候没有任何区别、
向量的创建:

 矩阵的创建:
矩阵的创建:

 特殊变量和常数:
特殊变量和常数:
 算术运算符:
算术运算符:
 关系运算符:
关系运算符:
 逻辑运算符:
逻辑运算符:
 其他常用符号
其他常用符号
 MATLAB的工作方式:
MATLAB的工作方式:



 常用函数:
常用函数:


 例:用图形表示连续调制波形y=sin(t)sin(9t)及其包络。
例:用图形表示连续调制波形y=sin(t)sin(9t)及其包络。
 (2)MATLAB在DSP中的应用
(2)MATLAB在DSP中的应用
 例:产生一个幅度为2,频率为4HZ,相位为π/6的正弦信号:
例:产生一个幅度为2,频率为4HZ,相位为π/6的正弦信号:
 例:产生一个高度为1,宽度为3,延时为2s的矩阵脉冲信号:
例:产生一个高度为1,宽度为3,延时为2s的矩阵脉冲信号:
 例:取样函数:用sinc(x)命令
例:取样函数:用sinc(x)命令
 例:产生均匀分布的白噪声,randn产生高斯分布的白噪声信号:
例:产生均匀分布的白噪声,randn产生高斯分布的白噪声信号:
 产生一个幅度为2, 频率为4HZ,相位为π/6的正弦信号:
产生一个幅度为2, 频率为4HZ,相位为π/6的正弦信号:
 产生单位脉冲序列m[n]和单位跃阶序列u[n-3]
产生单位脉冲序列m[n]和单位跃阶序列u[n-3]
 计算两个序列的卷积:
计算两个序列的卷积:




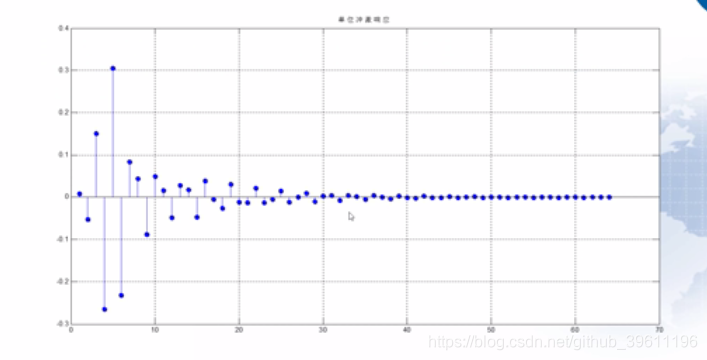
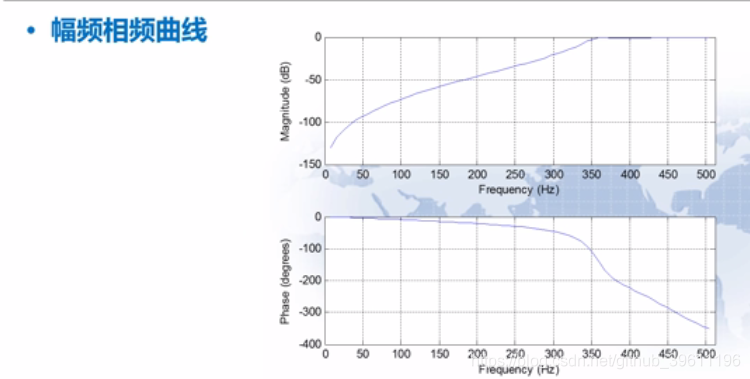
 DSP(数字信号处理)相对于ASP(模拟信号处理)的优点:(1)DSP对噪声和温度比较不敏感;(2)DSP具有更高的精度;(3)DSP更容易集成
DSP(数字信号处理)相对于ASP(模拟信号处理)的局限性:A/D D/A转换速率在某些场景下无法达到使用要求。
二、MATLAB基础及其在DSP中的应用
(1)MATLAB基础
在MATLAB中,数组、矩阵与向量在创建和显示的时候没有任何区别、
向量的创建:
DSP(数字信号处理)相对于ASP(模拟信号处理)的优点:(1)DSP对噪声和温度比较不敏感;(2)DSP具有更高的精度;(3)DSP更容易集成
DSP(数字信号处理)相对于ASP(模拟信号处理)的局限性:A/D D/A转换速率在某些场景下无法达到使用要求。
二、MATLAB基础及其在DSP中的应用
(1)MATLAB基础
在MATLAB中,数组、矩阵与向量在创建和显示的时候没有任何区别、
向量的创建:
t = 0:1:10
输出:

 矩阵的创建:
矩阵的创建:
a = [1 2 3; 4 5 6; 7 8 9]
输出:

 特殊变量和常数:
特殊变量和常数:
 算术运算符:
算术运算符:
 关系运算符:
关系运算符:
 逻辑运算符:
逻辑运算符:
 其他常用符号
其他常用符号
 MATLAB的工作方式:
MATLAB的工作方式:



 常用函数:
常用函数:


 例:用图形表示连续调制波形y=sin(t)sin(9t)及其包络。
例:用图形表示连续调制波形y=sin(t)sin(9t)及其包络。
t=(0:pi/100:pi)'; %长度为101的时间采样列向量
y1=sin(t)*[1,-1];% 包络线函数值,是(101x2)的矩阵
y2 = sin(t).*sin(9*t); %长度为101的调制波列向量
t3 = pi * (0: 9)/9;
y3 = sin(t3).*sin(9*t3);
plot(t, y1, 'r:', t, y2, 'b', t3, y3, 'bo');
axis([0, pi, -1, 1]) % 控制轴的范围
 (2)MATLAB在DSP中的应用
(2)MATLAB在DSP中的应用
 例:产生一个幅度为2,频率为4HZ,相位为π/6的正弦信号:
例:产生一个幅度为2,频率为4HZ,相位为π/6的正弦信号:
A = 2;
f = 4;
phi = pi / 6;
w0 = 2 * pi * f;
t = 0: 0.01:1;
x = A * sin(w0 * t + phi);
plot(t, x);
 例:产生一个高度为1,宽度为3,延时为2s的矩阵脉冲信号:
例:产生一个高度为1,宽度为3,延时为2s的矩阵脉冲信号:
t = 2: 0.02: 6;
plot(t, rectpuls(t-2, 3));
axis([-2, 6, 0, 1.5]);
 例:取样函数:用sinc(x)命令
例:取样函数:用sinc(x)命令
N = 1000;
t = -10: 20 / N: 10;
x = sinc(t /pi);
plot(t, x); grid on
 例:产生均匀分布的白噪声,randn产生高斯分布的白噪声信号:
例:产生均匀分布的白噪声,randn产生高斯分布的白噪声信号:
t = 0: 0.01: 1;
y = randn(1, length(t));
plot(t, y); grid on;
 产生一个幅度为2, 频率为4HZ,相位为π/6的正弦信号:
产生一个幅度为2, 频率为4HZ,相位为π/6的正弦信号:
A = 2;
phi = pi / 6;
omega = 2 * pi / 12;
n = -10:10;
x = A * sin(omega * n + phi);
stem(n, x, 'fill');
grid on;
 产生单位脉冲序列m[n]和单位跃阶序列u[n-3]
产生单位脉冲序列m[n]和单位跃阶序列u[n-3]
n = -2: 30;
x = [zeros(1, 5), 1, zeros(1, 27)];
y = [zeros(1, 5), ones(1, 28)];
subplot(2, 1, 1);
stem(n, x, 'fill'); grid on;
subplot(2, 1, 2);
stem(n, y, 'fill'); grid on;
 计算两个序列的卷积:
计算两个序列的卷积:
a = [-2 0 1 -1 3]
b = [1 2 0 -1];
c = conv(a, b);
M = length(c) - 1;
n = 0: 1: M;
stem(n, c, 'fill'); grid on;xlabel('Time index n');





