0.不讨论复杂情况的解释
对于一般的二次同余方程形如
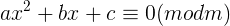
可以通过配方化为下式
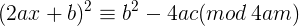
可通过换元,得到
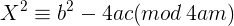
解出X的取值,然后用2ax+b回带,用扩展欧几里得解线性同余方程就可以得到方程本来的解
注意上式得到了一般二次同余方程的形式,即
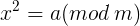
下文讨论上式的一般解法,并给出代码进行解释 1.朴素的二次同余方程的解法
因为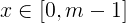 ,因此很明显可以直接枚举。时间复杂度
,因此很明显可以直接枚举。时间复杂度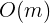 ,如果m稍微大一些效率就会很低
2.对于1的第一个优化
,如果m稍微大一些效率就会很低
2.对于1的第一个优化
由数论知识可得,对于0中的方程,我们可以分解m的质因数,即
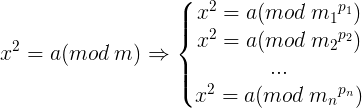
对于每一个方程,用1中的朴素解法来暴力枚举,时间复杂度优化到了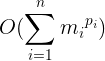
然后对于同余方程组的每一组解都做一个中国剩余定理就可以求得x 3.对于1的第二个优化
由数论知识可得,方程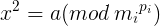 的解数为(假设方程有解):
的解数为(假设方程有解):
当mi为奇质数时,方程有2个解,假设一个是x0,则另一个是mi^pi-x0
当mi等于2且pi大于2时,方程有4个解,假设一个是x0,则另外三个是mi^pi-x0,x0+mi^(pi-1),mi^(pi-1)-x0
因此,如果原方程有解,那么只要枚举到一个解,那么就可以返回了。 4.对于2的优化
由2得,即使分解了质因数,但要枚举质因数的幂还是太困难,还是容易超时
对于2中同余方程组的一个方程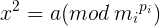 ,考虑这个方程
,考虑这个方程 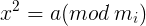 ,假设我们求出了这个方程的一个解x0,那么就可以解出这个方程
,假设我们求出了这个方程的一个解x0,那么就可以解出这个方程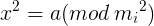 的一个解。
的一个解。
具体方法是在求出了x0之后,有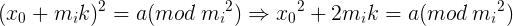
这是一个线性同余方程了,解出k的值,可得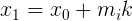 ,x1是方程
,x1是方程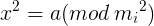 的一个解。
的一个解。
这样一直推下去,可以得到原方程的一个解。
利用3中结论,可得另外的解。
而解一个二次同余方程模质数,还是采用1中的枚举法,这样时间复杂度是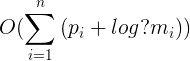 5.对于4的优化
5.对于4的优化
实际上,解一个二次同余方程模奇质数的方法以及很普遍了,不懂的可以看看大神acdreamers的博客http://blog.csdn.net/acdreamers/article/details/10182281。
对于模2的情况,这个直接枚举就行了。
有一个小优化,详见代码。 6.代码
因为现在我没有在网上找到哪个题可以交二次同余方程模合数的。。因此现在代码可能有bug。
对于一般的二次同余方程形如
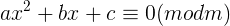
可以通过配方化为下式
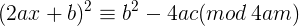
可通过换元,得到
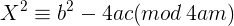
解出X的取值,然后用2ax+b回带,用扩展欧几里得解线性同余方程就可以得到方程本来的解
注意上式得到了一般二次同余方程的形式,即
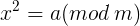
下文讨论上式的一般解法,并给出代码进行解释 1.朴素的二次同余方程的解法
因为
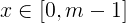 ,因此很明显可以直接枚举。时间复杂度
,因此很明显可以直接枚举。时间复杂度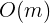 ,如果m稍微大一些效率就会很低
2.对于1的第一个优化
,如果m稍微大一些效率就会很低
2.对于1的第一个优化 由数论知识可得,对于0中的方程,我们可以分解m的质因数,即
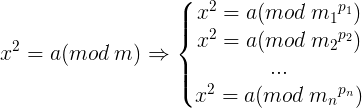
对于每一个方程,用1中的朴素解法来暴力枚举,时间复杂度优化到了
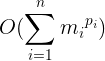
然后对于同余方程组的每一组解都做一个中国剩余定理就可以求得x 3.对于1的第二个优化
由数论知识可得,方程
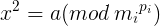 的解数为(假设方程有解):
的解数为(假设方程有解): 当mi为奇质数时,方程有2个解,假设一个是x0,则另一个是mi^pi-x0
当mi等于2且pi大于2时,方程有4个解,假设一个是x0,则另外三个是mi^pi-x0,x0+mi^(pi-1),mi^(pi-1)-x0
因此,如果原方程有解,那么只要枚举到一个解,那么就可以返回了。 4.对于2的优化
由2得,即使分解了质因数,但要枚举质因数的幂还是太困难,还是容易超时
对于2中同余方程组的一个方程
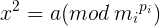 ,考虑这个方程
,考虑这个方程 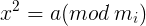 ,假设我们求出了这个方程的一个解x0,那么就可以解出这个方程
,假设我们求出了这个方程的一个解x0,那么就可以解出这个方程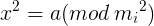 的一个解。
的一个解。 具体方法是在求出了x0之后,有
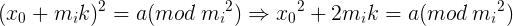
这是一个线性同余方程了,解出k的值,可得
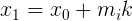 ,x1是方程
,x1是方程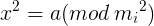 的一个解。
的一个解。 这样一直推下去,可以得到原方程的一个解。
利用3中结论,可得另外的解。
而解一个二次同余方程模质数,还是采用1中的枚举法,这样时间复杂度是
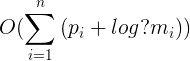 5.对于4的优化
5.对于4的优化 实际上,解一个二次同余方程模奇质数的方法以及很普遍了,不懂的可以看看大神acdreamers的博客http://blog.csdn.net/acdreamers/article/details/10182281。
对于模2的情况,这个直接枚举就行了。
有一个小优化,详见代码。 6.代码
因为现在我没有在网上找到哪个题可以交二次同余方程模合数的。。因此现在代码可能有bug。
#include*=p;
nowp*=p;
ll d,x,y,c;
c=((a-w*w)%nowp+nowp)%nowp;
exgcd(2*w*prep,nowp,d,x,y);
if(c%d==0)w=(w+(c/d*x%nowp+nowp)%(nowp/d)*prep)%nowp;
else return -1;
}
return w;
}
ll CRT()//合并方程组
{
ll res=0;
for(int i=0;ix,y,d,Mi=n/m[i];
exgcd(Mi,m[i],d,x,y);
res=(res+Mi*x*tempa[i])%n;
}
if(res<0)res+=n;
return res;
}
void dfs(int pos)//决定选取哪些方程做CRT
{
if(pos==cnt)
{
ans[++ans[0]]=CRT();
return;
}
m[pos]=pow(fac[pos][0],fac[pos][1],n+1);
for(int i=0;ipos][19];++i)
{
tempa[pos]=eqans[pos][i];
dfs(pos+1);
}
}
void quadratic_congruence()//二次同余主函数
{
for(int i=0;i0],fac[i][1],n+1),t=solve(a%p,fac[i][0],fac[i][1]);
if(t==-1)//如果有一个无解就返回
{
puts("No Solution");
return;
}
sets;
set::iterator iter;
if(t==0)//以前的程序有bug,如果整除的话那么不只有2或4个解
{
ll pp=pow(fac[i][0],(fac[i][1]+1)/2,n+1);
for(int i=0;pp*is.insert(pp*i);
}
else
{
s.insert(t);
s.insert(p-t);
if(fac[i][0]==2&&fac[i][1]>1)s.insert((t+p/2)%p);
if(fac[i][0]==2&&fac[i][1]>1)s.insert(((p/2-t)+p)%p);
}
for(iter=s.begin();iter!=s.end();iter++)
eqans[i][eqans[i][19]++]=*iter;
}
dfs(0);
}
int main()
{
scanf("%I64d%I64d",&a,&n);
frac(n);
quadratic_congruence();
sort(ans+1,ans+ans[0]+1);
for(int i=1;i<=ans[0];++i)
printf("%I64d%c",ans[i],i==ans[0]?'
':' ');
}