什么是CRC校验？

CRC校验即循环冗余校验。它可以发现并纠正信息在存储或传送过程中连续出现的多位错误码。
CRC码是基于模2运算而建立编码规律的校验码。其规律如下：
1）、模2加和模2减的结果相同的。（1±0 = 1、1±1 = 0、0±1 = 1、1±1 = 0）
2）、模2乘是按模2和求部分积之和。

3）、模2除是按模2减求部分余数。每求一位商应使部分余数减少一位。上商的原则是：当部分余数的位数小于除数的位数时，该余数即为最后余数。

---

如何进行CRC校验？

循环冗余校验同其他差错检测方式一样，通过在要传输的k比特数据D后添加(n-k)比特冗余位(又称帧检验序列，Frame Check Sequence，FCS)F形成n比特的传输帧T，再将其发送出去。 校验码格式
循环冗余校验提供一个预先设定的(n-k+1)比特整数P，并且要求添加的(n-k)比特F满足：
T mod P == 0 ……(1)
T = 2n-kD + F …… (2) 基于上述要求，实际应用时，发送方和接收方按以下方式通信：
1. 发送方和接收方在通信前，约定好预设整数P。
2. 发送方在发送前通过(1)和(2)式确定并填充F，然后发送。
3. 接收方收到数据，进行 result = T mod P 运算，当且仅当result = 0时接收方认为没有差错。 发送方在发送数据前需要确定填充的(n-k)比特F，以下提供了两种等价的方式来确定F。
（1）模二运算
模二运算采用无进位的二进制加法，恰好为异或(XOR)操作。
由于我们最终的目的是(1)式，根据(2)式，我们有
(2n-kD + F)/P = 2n-kD / P + F / P …… (3)
现在，我们令
2n-kD / P = Q + R / P …… (4)
于是，我们有
(2n-kD + F) / P = Q + R / P+ F / P …… (5)
由于采用无进位的二进制加法(等价于XOR操作)，因此当我们令 F = R 时，即T = 2n-kD + R，有
(2n-kD + F) / P = Q + R / P+ F / P = Q …… (6)
此时便有(1)式成立。
因此利用模二加法我们知，我们需要添加的帧检验序列F为：
F = 2n-kD modP …… (7) （2）二进制系数多项式
该种方法，我们试图对任意的二进制数都构造与其对应的一个二进制系数多项式，构造如下：
对于任意k位二进制数D =dk-1…d2d1d0，其对应的多项式为
D(X) = ∑di*Xi，i∊[0, k) …… (8)
例如，D = 110101，则D(X) = X5 + X4 + X2 + 1。
运算过程依然是模二的，则此时的CRC过程可描述如下：
Xn-kD(X) / P(X) = Q(X) + R(X) / P(X) …… (9)
T(X) = Xn-kD(X) + R(X) …… (10)
即，此时的F(X)满足：
F(X) = Xn-kD(X) mod P(X) …… (11) CRC的编码方法：
设待编码组的信息码组为Dn-1Dn-2…D2D1D0，共n位，它可用多项式M(x）表示：
M(x) = Dn-1xn-1 + Dn-2xn-2 + …… +D1X1 + D0x0（x后面的是次方）
将信息码组左移k位，得M(x)·xk，即成n+k位信息码组：
D n-1+k Dn-2+k……D2+kD1+kD0+k（000…00）k位
空出的k位用来拼接k位校验位。
CRC码就是用多项式M(x)·xk除以生成多项式G(x)（即产生校验码的多项式），所得余数作为校验码。为了得到k位余数，G(x)必须是k+1位。
设所得余数为R(x)，商为Q(x)，则有
M(X)·xk = Q(x)·G(x) + R(x)
将余数拼接在左移了k位后的信息位后面，就构成了这个有效信息的CRC码。这个CRC码用多项式表示为
M(X)·xk + R(x) = [Q(x)·G(x)+ R(x)]+ R(x)
= [Q(x)·G(x)]+ [R(x) +R(x)]
= Q(x)·G(x)
因此，所得CRC码是一个可被生成多项式G(x)除尽的数码。如果CRC码在传输过程中不出错，其余数必为0，如果传输过程中出错，则余数不为0，再由该余数指出哪一位出错，即可纠正。

---

CRC校验的例子

一致有效信息为1100，试用生成多项式G(x) = 1011将其编成CRC码。 解：有效信息M(x) = 1100 = x3 + x2 (n = 4)
由： G(x) = 1011 = x3 +x +1
得 k+1 = 4
k = 3
将有效信息左移3位后再被G(x)模2除，即：
M(x)·x3 = 1100000 = x6 +x5

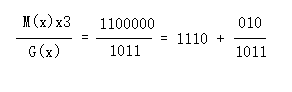
所以，M(x)·x3 +R(x) = 1100000 + 010 = 1100010为CRC码
总的信息为7位，有效信息为4位，所以又称（7,4）码。