题目地址:51Nod 1135
1.原根定义:设m>1,gcd(a,m)=1,使得 成立的最小的r,称为a对模m的阶。
成立的最小的r,称为a对模m的阶。
2.定理:如果模m有原根,那么他一共有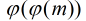 个原根。
个原根。
3.定理:如果p为素数,那么素数p一定存在原根,并且模p的原根的个数为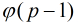 个。
个。
4.定理:假设m是正整数,a是整数,如果a模m的阶等于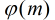 ,则称a为模m的一个原根。
,则称a为模m的一个原根。
5.模m有原根的充要条件:m=2,4,P^a,2*P^a…….
求模素数P的原根的方法:对P-1素因子分解,即P-1=(P1^a1)(P2^a2)…..(Pk^ak)。,若恒有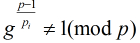 成立,那么g就是P的原根(对于合数而言,只需要把p-1换成
成立,那么g就是P的原根(对于合数而言,只需要把p-1换成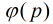 即可)
即可)
1.原根定义:设m>1,gcd(a,m)=1,使得
 成立的最小的r,称为a对模m的阶。
成立的最小的r,称为a对模m的阶。2.定理:如果模m有原根,那么他一共有
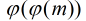 个原根。
个原根。3.定理:如果p为素数,那么素数p一定存在原根,并且模p的原根的个数为
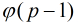 个。
个。4.定理:假设m是正整数,a是整数,如果a模m的阶等于
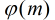 ,则称a为模m的一个原根。
,则称a为模m的一个原根。5.模m有原根的充要条件:m=2,4,P^a,2*P^a…….
求模素数P的原根的方法:对P-1素因子分解,即P-1=(P1^a1)(P2^a2)…..(Pk^ak)。,若恒有
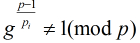 成立,那么g就是P的原根(对于合数而言,只需要把p-1换成
成立,那么g就是P的原根(对于合数而言,只需要把p-1换成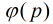 即可)
即可)
#include if(pri[i]) {
prime[k++]=i;
for(int j=i+i; j0;
}
}
}
void Divide(int n)//将n分解为素因子
{
cnt=0;
int t=(int)sqrt(1.0*n);
for(int i=0; prime[i]<=t; i++) {
if(n%prime[i]==0) {
sprime[cnt++]=prime[i];
while(n%prime[i]==0)//因为有可能有多个peime[i]
n/=prime[i];
}
}
if(n>1)
sprime[cnt++]=n;//可能只有自己一个素因子
}
LL modexp(LL a,LL b,int mod)//快速幂取余
{
LL res=1;
while(b>0) {
a=a%mod;
if(b&1)
res=res*a%mod;
b=b>>1;
a=a*a%mod;
}
return res;
}
int main()
{
int p;
is_prime();
while(~scanf("%d",&p)) {
Divide(p-1);
for(int g=2; gint flag=1;
for(int i=0; iint t=(p-1)/sprime[i];
if(modexp(g,t,p)==1) {
flag=0;
break;
}
}
if(flag) {
int root=g;
printf("%d
",root);
break;//去掉break的话是求所有的原根,加上break是求最小的原根、
}
}
}
return 0;
}