上学期做过激光平行平面腔的自再现模研究,基于Matlab,采用Fox-Li数值迭代法得到条形平面腔的稳定输出模式。得到振幅分布曲线如下: 但由于对Matlab图片动画显示并不熟悉,最近便想能否用安卓来实现,通过不断重新加载UI,使分布曲线随着迭代次数动态改变。本来以为应该是对公式进行简单输入就能实现,做起来才发现还是有不少麻烦的,不过还好,最终还是把效果做出来了。
先介绍自再现模的迭代公式:
但由于对Matlab图片动画显示并不熟悉,最近便想能否用安卓来实现,通过不断重新加载UI,使分布曲线随着迭代次数动态改变。本来以为应该是对公式进行简单输入就能实现,做起来才发现还是有不少麻烦的,不过还好,最终还是把效果做出来了。
先介绍自再现模的迭代公式:
 u(x)就是要求的稳定模式,先把u(x)设为1,然后代入公式求出新的u(x),继续不断回代,进行数值迭代,当u(x)的整体分布不再改变时,就得到了自再现模。其中a为腔镜半宽度,L为腔长,k是波矢量。具体迭代操作就是,将-a到a的积分区间分割,初始u(x)=1,要求新的u(x),就是对[-a,a]上每一分割点都基于公式,将积分转换为累加计算得到,对得到的u(x)回代又能得到新的u(x),设置迭代100次,基本就能得到稳定的分布。
下面介绍在android上该迭代过程的具体操作。先定义要用到的各个变量。发现,这里的数据都是复数型的,而Java没有这种数据类型,所以只能自己定义复数类,实际就是在这个类中包含两个double类型数据,一个表示实部,一个表示虚部,和各种方法用于后面进行操作,根据需要,我设置的方法有,重写toString方法、加法运算、乘法运算(为操作方便分别定义了与复数间的和与实数间的乘法)、以及实部与虚部数据的get和set。代码如下:
u(x)就是要求的稳定模式,先把u(x)设为1,然后代入公式求出新的u(x),继续不断回代,进行数值迭代,当u(x)的整体分布不再改变时,就得到了自再现模。其中a为腔镜半宽度,L为腔长,k是波矢量。具体迭代操作就是,将-a到a的积分区间分割,初始u(x)=1,要求新的u(x),就是对[-a,a]上每一分割点都基于公式,将积分转换为累加计算得到,对得到的u(x)回代又能得到新的u(x),设置迭代100次,基本就能得到稳定的分布。
下面介绍在android上该迭代过程的具体操作。先定义要用到的各个变量。发现,这里的数据都是复数型的,而Java没有这种数据类型,所以只能自己定义复数类,实际就是在这个类中包含两个double类型数据,一个表示实部,一个表示虚部,和各种方法用于后面进行操作,根据需要,我设置的方法有,重写toString方法、加法运算、乘法运算(为操作方便分别定义了与复数间的和与实数间的乘法)、以及实部与虚部数据的get和set。代码如下:


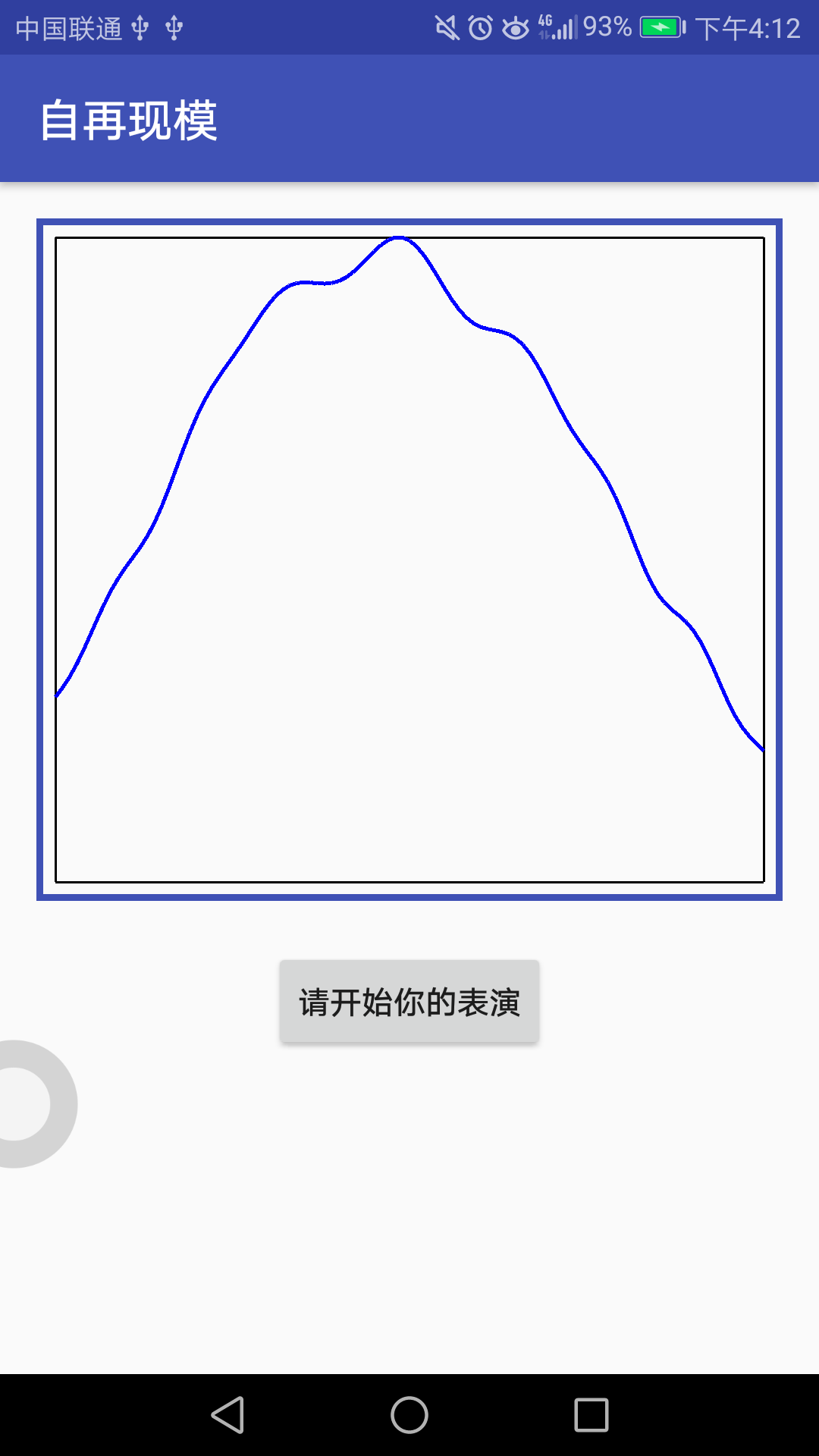
 后面还可以通过设置编辑框来改变镜宽和腔长等参量,进一步观察效果,以及绘制坐标值等。
后面还可以通过设置编辑框来改变镜宽和腔长等参量,进一步观察效果,以及绘制坐标值等。
 但由于对Matlab图片动画显示并不熟悉,最近便想能否用安卓来实现,通过不断重新加载UI,使分布曲线随着迭代次数动态改变。本来以为应该是对公式进行简单输入就能实现,做起来才发现还是有不少麻烦的,不过还好,最终还是把效果做出来了。
先介绍自再现模的迭代公式:
但由于对Matlab图片动画显示并不熟悉,最近便想能否用安卓来实现,通过不断重新加载UI,使分布曲线随着迭代次数动态改变。本来以为应该是对公式进行简单输入就能实现,做起来才发现还是有不少麻烦的,不过还好,最终还是把效果做出来了。
先介绍自再现模的迭代公式:
 u(x)就是要求的稳定模式,先把u(x)设为1,然后代入公式求出新的u(x),继续不断回代,进行数值迭代,当u(x)的整体分布不再改变时,就得到了自再现模。其中a为腔镜半宽度,L为腔长,k是波矢量。具体迭代操作就是,将-a到a的积分区间分割,初始u(x)=1,要求新的u(x),就是对[-a,a]上每一分割点都基于公式,将积分转换为累加计算得到,对得到的u(x)回代又能得到新的u(x),设置迭代100次,基本就能得到稳定的分布。
下面介绍在android上该迭代过程的具体操作。先定义要用到的各个变量。发现,这里的数据都是复数型的,而Java没有这种数据类型,所以只能自己定义复数类,实际就是在这个类中包含两个double类型数据,一个表示实部,一个表示虚部,和各种方法用于后面进行操作,根据需要,我设置的方法有,重写toString方法、加法运算、乘法运算(为操作方便分别定义了与复数间的和与实数间的乘法)、以及实部与虚部数据的get和set。代码如下:
u(x)就是要求的稳定模式,先把u(x)设为1,然后代入公式求出新的u(x),继续不断回代,进行数值迭代,当u(x)的整体分布不再改变时,就得到了自再现模。其中a为腔镜半宽度,L为腔长,k是波矢量。具体迭代操作就是,将-a到a的积分区间分割,初始u(x)=1,要求新的u(x),就是对[-a,a]上每一分割点都基于公式,将积分转换为累加计算得到,对得到的u(x)回代又能得到新的u(x),设置迭代100次,基本就能得到稳定的分布。
下面介绍在android上该迭代过程的具体操作。先定义要用到的各个变量。发现,这里的数据都是复数型的,而Java没有这种数据类型,所以只能自己定义复数类,实际就是在这个类中包含两个double类型数据,一个表示实部,一个表示虚部,和各种方法用于后面进行操作,根据需要,我设置的方法有,重写toString方法、加法运算、乘法运算(为操作方便分别定义了与复数间的和与实数间的乘法)、以及实部与虚部数据的get和set。代码如下:
public class Complex {
private double real;
private double img;
public Complex(double real,double img){
this.real = real;
this.img = img;
}
public Complex(double real){
this.real = real;
img = 0;
}
public Complex(){
real = 0;
img = 0;
}
@Override
public String toString() {
return real+" + "+img+"i";
}
public Complex plus(Complex b){
return new Complex(this.real+b.real,this.img+b.img);
}
public Complex multiply(double b){
return new Complex(this.real*b,this.img*b);
}
public Complex multiply(Complex c) {
double a = this.real;
double b = this.img;
double d = c.getReal();
double e = c.getImg();
return new Complex(a * d - b * e, a * e + b * d);
}
public double getReal(){
return this.real;
}
public double getImg(){
return this.img;
}
public void setReal(double real){
this.real = real;
}
public void setImg(double img){
this.img = img;
}
}
复数有了,我们就需要定义数组u以存放每次迭代的数据结果,由于数组只能用于基本类型,没办法,我们只能采用 ArrayList了,定义完还需全部置1,即:使u(x)初始为1。接着,做着做着就发现,Math里面的exp方法在这里是用不了的,因为是对复数进行操作的,那只能自己定义了。想了一下,可以基于欧拉公式:exp(a+bi)=exp(a)*(cosb+isinb)。代码如下:
public Complex exp(Complex c){
Complex result = new Complex();
double a = c.getReal();
double b = c.getImg();
double expa = Math.exp(a);
result.setImg(expa*Math.sin(b));
result.setReal(expa*Math.cos(b));
return result;
}做着做着又发现,公式中还有对复数进行开根号的运算,同样Math里面的sqrt又不能用,还是得自己定义。又是新的麻烦,好在回想起以前是怎么对复数开根:要求sqrt(a+bi),可先令(m+ni)*(m+ni)=a+bi,得到a=m2-n2,b=2mn,顺着求解得到m和n用a和b表达的公式就行了。代码如下:
public Complex sqrt(Complex c){
Complex result = new Complex();
double a = c.getReal();
double b = c.getImg();
//result = m + ni;
double m = Math.sqrt((a+Math.sqrt(a*a+b*b))/2);
double n = b/(2*m);
result.setReal(m);
result.setImg(n);
return result;
}接下来还要定义求复数模abs()方法、求归一化normalize()方法,因为我们是要得到自再现模的场分布大致不变,所以需要进行归一化。定义完就能按照公式进行迭代计算了。
完成上面数据计算工作,为了绘制曲线,就需要自定义View,以实现绘制振幅曲线。具体就是将前面计算得到的[-a,a]间的每一分割点的振幅大小显示出来。先把x轴上每一分割点与相应的y坐标一一对应起来,注意,y轴是屏幕由上向下增大的,为方便观看,应当是振幅越大,y坐标值越小。然后调用canvas的drawLine方法连接每个点,得到曲线。
在MainActivity中,自定义一个线程,实现每完成一次迭代计算,更新一次主线程UI显示就能实现迭代过程的振幅分布曲线动态显示。效果如下:



 后面还可以通过设置编辑框来改变镜宽和腔长等参量,进一步观察效果,以及绘制坐标值等。
后面还可以通过设置编辑框来改变镜宽和腔长等参量,进一步观察效果,以及绘制坐标值等。