先说一下题目,要求必须用python完成,看了老师的代码,嗯……,还是自己写吧
 直接撸代码,最后再说知识点。
环境:python3.6 + pycharm
直接撸代码,最后再说知识点。
环境:python3.6 + pycharm

 x^6 +x^4+x^2+x+1转换为10100111(这里我就不逆序写了),x^7+x+1转换为10000011,然后直接异或就行了。
2 乘法部分
x*f(x)=
x^6 +x^4+x^2+x+1转换为10100111(这里我就不逆序写了),x^7+x+1转换为10000011,然后直接异或就行了。
2 乘法部分
x*f(x)=
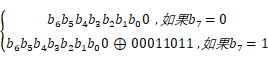 记住这个公式,先说一下00011011怎么来的,因为x^8(mod m(x)) = [m(x)-x^8] = x^4+x^3+x+1),转换为二进制就是00011011了,是不是感觉贼扯淡了...,别急,后面还有更扯淡的
因为g(x)可以化为(00000001
记住这个公式,先说一下00011011怎么来的,因为x^8(mod m(x)) = [m(x)-x^8] = x^4+x^3+x+1),转换为二进制就是00011011了,是不是感觉贼扯淡了...,别急,后面还有更扯淡的
因为g(x)可以化为(00000001 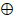 00000010
00000010  10000000),所以本来的乘法就化成了f(x)跟化简完的式子相乘,这时候想想上面的式子,x是00000001,将x不断带入,是不是套公式就行了,连mod都省了,这里有个重点就是先移位,记住,是先移位!然后再根据b7的值决定是不是要跟m(x)异或。
整道题比较难的部分就是那个乘法公式不怎么好写,但归根结底两个公式,一个异或,一个上面那个公式,还有就是异或会不断复用,
10000000),所以本来的乘法就化成了f(x)跟化简完的式子相乘,这时候想想上面的式子,x是00000001,将x不断带入,是不是套公式就行了,连mod都省了,这里有个重点就是先移位,记住,是先移位!然后再根据b7的值决定是不是要跟m(x)异或。
整道题比较难的部分就是那个乘法公式不怎么好写,但归根结底两个公式,一个异或,一个上面那个公式,还有就是异或会不断复用,就别作死懒得写函数直接拿头解了,别问我怎么知道的。
等以后有空再修改一下,感觉有地方说的不够详细。
 直接撸代码,最后再说知识点。
环境:python3.6 + pycharm
直接撸代码,最后再说知识点。
环境:python3.6 + pycharm
#多项式加法
def add(a,b):
a = list(map(int, a))
b = list(map(int, b))
c=[0,0,0,0,0,0,0,0]
for i in range(8):
if(a[i] == b[i]):
c[i]=0
else:
c[i]=1
return list(map(int, c))
#多项式乘法,取个好名好养活哈哈
def cheng(a,b):
#将a,b从字符串转换为int类型
a = list(map(int, a))
b = list(map(int, b))
#前面直接用c=[a]*8会导致一个数组的变化引起其他数组的变化
c=[[1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 1, 0, 1, 0]] #为了进行a和b的异或,需要八个数组
#异或用的数组
c2 = [1,1,0,1,1,0,0,0]
c2 = list(map(int, c2))
list2=[]
for i in range(8): #判断b中1的位置,然后对c中对应位置进行移位
if(b[i]==1):
list2.append(i) #记录需要异或的位置
#开始进行乘法运算
for j in range(i):
if c[i][7] == 1: #判断b7是否为1,是则先移位,然后与c2异或
for k in range(7):
c[i][7-k] = c[i][7-k-1]
if k+1 == 7:
c[i][0] = 0
c[i] = add(c[i],c2)
else: #若b7不为1,则直接进行移位
for h in range(7):
c[i][7-h] = c[i][7-h-1]
if h+1==7:
c[i][0] = 0
#将list2转换为int类型
list2 = list(map(int,list2))
#将结果存储到result内
result=c[list2[0]]
for i in range(len(list2)):
if i+1 == len(list2):
break
result = add(result,c[list2[i+1]])
return result
if __name__ == '__main__':
print("【格式:1 1 1 1 1 1 1 1】x的系数为0输入0,注意,请将二进制的高位靠后,低位靠前输入")
m1= input("输入第一个多项式 :")
m2 = input("输入第二个多项式【格式同上】 :")
# m1="1 1 1 0 1 0 1 0"
# m2="1 1 0 0 0 0 0 1"
a = m1.split(' ')
b = m2.split(' ')
print("注意,输出结果为逆序【变成过程中因为二进制高位的问题所以用逆序输出】")
print(add(a,b))
print(cheng(a,b))
介绍一下重要的知识点:
1 加法部分
先把多项式转换为二进制,
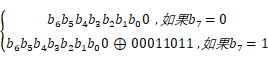 记住这个公式,先说一下00011011怎么来的,因为x^8(mod m(x)) = [m(x)-x^8] = x^4+x^3+x+1),转换为二进制就是00011011了,是不是感觉贼扯淡了...,别急,后面还有更扯淡的
因为g(x)可以化为(00000001
记住这个公式,先说一下00011011怎么来的,因为x^8(mod m(x)) = [m(x)-x^8] = x^4+x^3+x+1),转换为二进制就是00011011了,是不是感觉贼扯淡了...,别急,后面还有更扯淡的
因为g(x)可以化为(00000001