数学上,同余(英语:congruence modulo,符号:≡)是数论中的一种等价关系。当两个整数除以同一个正整数,若得相同余数,则二整数同余。同余是抽象代数中的同余关系的原型。最先引用同余的概念与“≡”符号者为德国数学家高斯。
定义:两个正整数a,b如果它们初一正整数m所得的余数相同,则称a,b对于模m同余。记作:
a≡b(mod m) 性质 性质1:a≡b(mod m) => c*m=a-b ,c属于Z(即是说 a 和 b 之差是 m 的倍数)
换句话说:a≡b(mod m) => m | (a-b) (即是说 m 能整除 a 和 b 之差,同时m | (a-b) 也是a,b关于m同余的充要条件) 性质2: 同余关系具有反身性、对称性与传递性,即
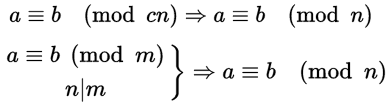
也即是说:m 的因数也可以整除(a-b)。
m是n的倍数: m = c *n , n | m , 因为m|(a-b) , 所以 n | (a-b) => a≡b (mod n) 同余关系式 威尔逊定理 威尔逊定理给出了判定一个自然数是否为素数的充分必要条件。
即:当且仅当p为素数时:(p-1)! ≡ -1 (mod p)
但是由于阶乘是呈爆炸增长的,其结论作为了解。 费马小定理 假如a是一个整数,p是一个质数,那么 是p的倍数,可以表示为a^p≡a (mod p) 当(a,p)=1 (a不是p的倍数) 时定理可以写为:a^(p-1) ≡1 (mod p) 费马小定理是欧拉定理的一个特殊情况,看下面 欧拉定理 欧拉定理(也称费马-欧拉定理或欧拉函数定理)是一个关于同余的性质:若 n,a为正整数,且 n,a互素(即 gcd(a,n)=1)则 a^φ(n) ≡1 (mod m) 即 a^φ(n)与1在模n下同余;φ(n)为欧拉函数。 当n是素数的时候, φ(n)=n-1,所以欧拉定理变为:
a^(n-1) ≡ 1 (mod m) or
a^n ≡ a (mod m)
这就是费马小定理。 卡迈克尔函数
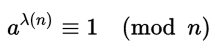 阶乘幂
阶乘幂
 REF:
REF:
知行执行
wikipedia
a≡b(mod m) 性质 性质1:a≡b(mod m) => c*m=a-b ,c属于Z(即是说 a 和 b 之差是 m 的倍数)
换句话说:a≡b(mod m) => m | (a-b) (即是说 m 能整除 a 和 b 之差,同时m | (a-b) 也是a,b关于m同余的充要条件) 性质2: 同余关系具有反身性、对称性与传递性,即
1)a≡a (mod m); 2)若a≡b (mod m), 则b≡a (mod m); 3)若a≡b (mod m), b≡c (mod m),则a≡c (mod m).性质3 :若a≡b(mod m), c≡d (mod m),则
1)a+c≡b+d (mod m); 2)a-c≡b-d (mod m); 3)ac≡bd (mod m). 推论 若a≡b(mod m),n为自然数,则an≡bn (mod m)。性质4 除法定理一:如果ka≡kb(mod m),且(m,k)=1(即k和m互质),则a≡b(mod m) 性质4 除法定理二:
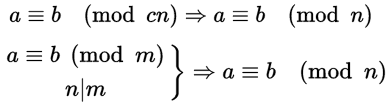
也即是说:m 的因数也可以整除(a-b)。
m是n的倍数: m = c *n , n | m , 因为m|(a-b) , 所以 n | (a-b) => a≡b (mod n) 同余关系式 威尔逊定理 威尔逊定理给出了判定一个自然数是否为素数的充分必要条件。
即:当且仅当p为素数时:(p-1)! ≡ -1 (mod p)
但是由于阶乘是呈爆炸增长的,其结论作为了解。 费马小定理 假如a是一个整数,p是一个质数,那么 是p的倍数,可以表示为a^p≡a (mod p) 当(a,p)=1 (a不是p的倍数) 时定理可以写为:a^(p-1) ≡1 (mod p) 费马小定理是欧拉定理的一个特殊情况,看下面 欧拉定理 欧拉定理(也称费马-欧拉定理或欧拉函数定理)是一个关于同余的性质:若 n,a为正整数,且 n,a互素(即 gcd(a,n)=1)则 a^φ(n) ≡1 (mod m) 即 a^φ(n)与1在模n下同余;φ(n)为欧拉函数。 当n是素数的时候, φ(n)=n-1,所以欧拉定理变为:
a^(n-1) ≡ 1 (mod m) or
a^n ≡ a (mod m)
这就是费马小定理。 卡迈克尔函数
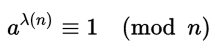 阶乘幂
阶乘幂  REF:
REF: 知行执行
wikipedia