[Unity3D学习]3D数学基础之向量

2014.05.11 向量是2D、3D数学研究的标准工具，在3D游戏中向量是基础。

一、向量

1、向量的数学定义

•  向量就是一个数字列表，对于程序员来说一个向量就是一个数组。
• 向量的维度就是向量包含的“数”的数目，向量可以有任意正数维，标量可以被认为是一维向量。
• 书写向量时，用方括号将一列数括起来，如[1,2,3] 水平书写的向量叫行向量 垂直书写的向量叫做列向量

2、向量的几何意义

• 几何意义上说，向量是有大小和方向的有向线段。向量的大小就是向量的长度（模）向量有非负的长度。
• 向量的方向描述了空间中向量的指向。
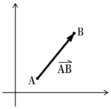
• 向量的形式：向量定义的两大要素——大小和方向，有时候需要引用向量的头和尾，下图所示，箭头是向量的末端，箭尾是向量的开始                                                                                                 
• 向量中的数表达了向量在每个维度上的有向位移，例如2D向量列出的是沿x坐标方向和y坐标方向的位移。

3、向量与点

• “点”有位置，但没有实际的大小或厚度，“向量”有大小和方向，但没有位置。所以使用“点”和“向量”的目的完全不同。”点”描述位置，“向量”描述位移。

4、点和向量的关系：任意一点都能用 从原点开始的向量来表达。

二、向量运算

1、零向量

• 零向量非常特殊，因为它是唯一大小为零的向量。对于其他任意数m,存在无数多个大小（模）为m的向量，他们构成一个圆。零向量也是唯一一个没有方向的向量。

2、负向量

• 负运算符也能应用到向量上。每个向量v都有一个加性逆元-v，它的维数和v一样，满足v+(-v)=0。要得到任意维向量的负向量，只需要简单地将向量的每个分量都变负即可。
• 几何解释：向量变负，将得到一个和向量大小相等，方向相反的向量。

3、向量大小（长度或模）

• 在线性代数中，向量的大小用向量两边加双竖线表示，向量的大小就是向量各分量平方和的平方根       ||v||=√(x^2+y^2)                    （2D向量v）                                                                                                           ||v||=√(x^2+y^2+z^2)           (3D向量v)
• 几何解释：在2D中的任意向量v，能构造一个以v为斜边的直接三角形，由勾股定理可知，对于任意直角三角形，斜边的长度平方等于两直角边长度的平方和。                                                                        ||v||^2 = x^2   +  y^2 

4、标量与向量的乘法

• 虽然标量与向量不能相加，但它们可以相乘。结果将得到一个向量。与原向量平行，但长度不同或者方向相反。
• 标量与向量的乘法非常直接，将向量的每个分量都与标量相乘即可。如：k[x,y,z] = [xk,yk,zk]
• 向量也能除以非零向量，效果等同于乘以标量的倒数。如：[x,y,z]/k = [x/k,y/k,z/k]

1. 标量与向量相乘时，不需要些乘号，将两个量挨着写即表示相乘。
2. 标量与向量的乘法和除法优先级高于加法和乘法
3. 标量不能除以向量，并且向量不能除以另一个向量。
4. 负向量能被认为是乘法的特殊情况，乘以标量-1。

• 几何解释:向量乘以标量k的效果是以因子|k|缩放向量的长度，例如：为了使向量的长度加倍，应使向量乘以2.如果k<0，则向量的方向被倒转。

5、标准化向量

• 对于许多向量，我们只关心向量的方向不在乎向量的大小，如：“我面向的是什么方向？”，在这样的情况下，使用单位向量非常方便，单位向量就是大小为1的向量，单位向量经常也被称作为标准化向量或者法线。
• 对于任意非零向量v，都能计算出一个和v方向相同的单位向量k,这个过程被称作向量的“标准化”，要标准化向量，将向量除以它的大小（模）即可。                                                                                    k=v/||v||,v!=0;
• 零向量不能被标准化，数学上这是不允许的，因为将导致除以零，几何上也没有意义，零向量没有方向。
• 几何解释：2D环境中，如果以原点为尾画一个单位向量，那么向量的头将接触到圆心在原点的单位圆。3D环境中单位向量将接触单位球。

6、向量的加法和减法

• 两个向量的维数相同，那么它们能相加，或者相减。结果向量的维数与原向量相同。向量加减法的记发和标量加减法的记法相同。例如：[x,y,z] + [a,b,c] = [x+a,y+b,z+c]
• 减法解释为加负向量，a-b=a+(-b) 例如： [x,y,z] – [a,b,c] = [x-a,y-b,c-z]
• 向量不能与标量或维数不同的向量相加减。
• 和标量加法一样，向量加法满足交换律，但向量减法不满足交换律，永远有a+b = b+a,但a-b=-(b-a),仅当a=b时，a-b = b-a
• 几何解释：向量a和向量b相加的几何解释为：平移向量，使向量a的头连接向量b的尾，接着从a的尾向b的头画一个向量。这就是向量加法的“三角形法则”。
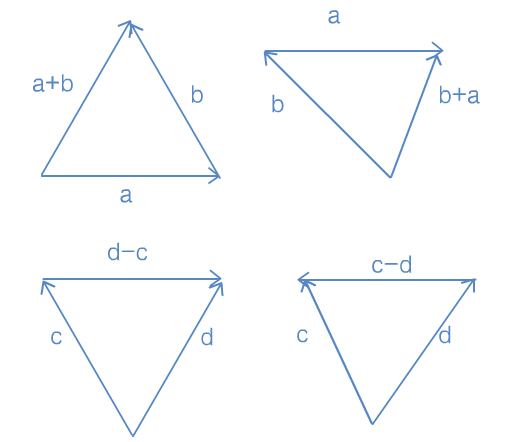
• 计算一个点到另一个点的位移是一种非常普遍的需求，可以使用三角形法则和向量减法来解决这个问题，如： 上图  d-c 计算出 c 到 d 的位移向量。

7、距离公式

• 距离公式用来计算两点之间的距离。从上面可以得知两点间的位移向量通过向量减法可以得知，既然得到了两点间的位移向量，那么求出位移向量的模，就能计算出两点间的位移。

8、向量点乘

• 标量和向量可以相乘，向量和向量也可以相乘。有两种不同类型的乘法，点乘、叉乘
• 点乘的记法来至a·b中的点。与标量和向量的乘法一样，向量点乘的优先级高于加法和减法。标量乘法和标量与向量的乘法可以省略乘号，但在向量点乘中不能省略点乘号。向量点乘就是对应分量乘积的和。其结果是一个标量.     [x,y,z] · [a,b,c] = ax+by+cz;
• 几何解释：一般来说，点乘结果描述了两个向量的“相似”程度，点乘结果越大，两个向量越相近，点乘和向量间的夹角相关 计算两向量间的夹角    θ = arccos(a·b)

9、向量投影

• 给定两个向量v和n,能够将v分解成两个分量， 它们分别垂直和平行于向量n，并且满足 两向量相加等于向量v，一般称平行分量为v在向量n上的投影。
• 平行分量公式： 平行分量 = n(v·n)/||n||^2
• 垂直分量公式:    垂直分量 = ||v|| –  n(v·n)/||n||^2

10、向量叉乘

• 向量叉乘得到一个向量，并且不满足交换律。  它满足反交换律 a × b =  -(b × a)                                           叉乘公式：[x,y,z] × [a,b,c] = [yc-zb , za-xc , xb-ya]
• 当点乘和叉乘在一起时，叉乘优先计算， a · b × c = a·(b×c)  因为点乘返回一个标量，同时标量和向量间不能叉乘。
• 几何解释：叉乘得到的向量垂直于原来的两个向量。
• a × b 的长度等于向量的大小与向量夹角sin值的积，||a × b|| = ||a|| ||b|| sinθ                               ||a × b||也等于以a和b为两边的平时四边形的面积。
• 叉乘最重要的应用就是创建垂直于平面、三角形、多边形的向量。

转载：http://blog.gamerisker.com/archives/347.html

Dot Product 点乘

The dot product takes two vectors and returns a scalar. This scalar is equal to the magnitudes of the two vectors multiplied together and the result multiplied by the cosine of the angle between the vectors. When both vectors are normalized, the cosine essentially states how far the first vector extends in the second's direction (or vice-versa - the order of the parameters doesn't matter). 两个向量想成的结果是一个标量。此标是等于两个向量长度相乘结果乘以向量之间的夹角的余弦。当两个向量都为单位向量时，余弦的定义就表示为第一个向量在第二个向量上面的射影长度（或反之亦然 - 参数的顺序并不重要） 。 It is easy enough to think in terms of angles and then find the corresponding cosines using a calculator. However, it is useful to get an intuitive understanding of some of the main cosine values as shown in the diagram below:- 容易想像，在角度方面可以通过计算器计算余弦值。然而，下面图标中的一些主要的余弦值是会经常用到的。 The dot product is a very simple operation that can be used in place of the Mathf.Cos function or the vector magnitude operation in some circumstances (it doesn't do exactly the same thing but sometimes the effect is equivalent). However, calculating the dot product function takes much less CPU time and so it can be a valuable optimization. 点程是一个非常简单的操作，可以在需要矢量长度操作的地方用Mathf.Cos功能（它不会做同样的事情，但有时效果是等价的）。尽管如此,计算点乘功能需要CPU时间要少得多，因此它可以是一个有价值的优化。

Cross Product 叉乘

The other operations are defined for 2D and 3D vectors and indeed vectors with any number of dimensions. The cross product, by contrast, is only meaningful for 3D vectors. It takes two vectors as input and returns another vector as its result. 其他操作被定义为二维和三维向量和任意维数向量。叉乘只能用来计算3D向量，它需要输入两个向量返回结果是另一个向量。 The result vector is perpendicular to the two input vectors. The "left hand rule" can be used to remember the direction of the output vector from the ordering of the input vectors. If the first parameter is matched up to the thumb of the hand and the second parameter to the forefinger, then the result will point in the direction of the middle finger. If the order of the parameters is reversed then the resulting vector will point in the exact opposite direction but will have the same magnitude. 得到的结果垂直于输入的两个向量。"左手坐标系"可以用来表示输入和输出的向量的方向。如果第一个参数匹配手的拇指和食指匹配第二个参数，结果将是中指的方向。如果参数的顺序是相反的结果向量将指向正好相反的方向，但将有相同长度。 The magnitude of the result is equal to the magnitudes of the input vectors multiplied together and then that value multiplied by the sine of the angle between them. Some useful values of the sine function are shown below:- 结果的大小等于输入向量的乘积，然后通过它们之间的角度的正弦值乘以该值的大小。 The cross product can seem complicated since it combines several useful pieces of information in its return value. However, like the dot product, it is very efficient mathematically and can be used to optimize code that would otherwise depend on slow transcendental functions. 叉乘比较复杂，因为在其返回值结合了一些有用的信息。但是像点乘那样,这些非常有效的数学可以用来优化代码，否则将依赖于缓慢的超越函数。
转载：http://game.ceeger.com/Manual/UnderstandingVectorArithmetic.html
一个向量在另一个向量方向的投影量值


汽车的里程表通常按车轮的旋转速度计算。汽车可能不是直接向前移动（如发生侧滑），这种情况下，部分运动是里程表无法测量的。对象 rigidbody.velocity 向量的量值使速度以总体运动方向为方向，但会脱离前进方向上的速度，此时应使用点积：-


var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);


当然，方向可以是您喜欢的任意方向，但方向向量应始终设为单位向量，以便进行计算。不仅结果比速度向量更准确，而且无需减缓平方根运算来计算量值。




在做rpg类游戏的过程中,经常遇到要判断周围怪物相对自身的方位


1.判断目标在自己的前后方位可以使用下面的方法:
   Vector3.Dot(transform.forward, target.position)
       返回值为正时,目标在自己的前方,反之在自己的后方


2.判断目标在机子的左右方位可以使用下面的方法:
   Vector3.Cross(transform.forward, target.position).y
      返回值为正时,目标在自己的右方,反之在自己的左方


3.在这里顺便解说下关于空间向量的点积和叉积:
A.点积 
  点积的计算方式为:  a·b=|a|·|b|cos  其中|a|和|b|表示向量的模，表示两个向量的夹角。另外在 点积 中，和 夹角是不分顺序的。 
  所以通过点积，我们其实是可以计算两个向量的夹角的。 
  另外通过点积的计算我们可以简单粗略的判断当前物体是否朝向另外一个物体: 只需要计算当前物体的transform.forward向量与 otherObj.transform.position 的点积即可， 大于0则在前方，否则在后方。
B.叉积 
  叉积的定义： c =a x b  其中a,b,c均为向量。即两个向量的叉积得到的还是向量！ 
  性质1： c⊥a，c⊥b，即向量c垂直与向量a,b所在的平面 。 
  性质2： 模长|c|=|a||b|sin 
  性质3： 满足右手法则 。从这点我们有axb ≠ bxa，而axb = – bxa。所以我们可以使用叉积的正负值来判断向量a，b的相对位置，即向量b是处于向量a的顺时针方向还是逆时针方向