《工程优化》课程总结之一 - 平头弟

《工程优化》课程总结之一

2019-04-13 15:33发布生成海报

站内文章 / 模拟电子

11377 0

《工程优化》课程总结题注：新年快来了，各种考试接踵而至，先将《工程优化》稍作总结。

第一章绪论第二章基本概念和理论基础第三章常用一维搜索方法第四章无约束最优化方法第五章线性规划第六章约束最优化方法
第一章：绪论 1.最优化问题两大要素：（1）可能方案（2）追求目标 2.按第一要素与时间的相关性分为：静态和动态最优化，本书（陈开周《工程优化方法》）主要专门讲述静态最优化问题。 3.数学模型：决策变量和参数，目标函数和约束或者限制条件。 4.按有无约束：无约束优化 vs. 有约束优化

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

vs.

5.可行解：满足所有约束条件的向量

；可行解的集合称为可行集。 6.目标函数的转换：求极大值将目标函数乘以（-1）化为求极小值。 7.模型的统一化：约束条件的转换（包括等式的转换）

8.按函数类型： 1）线性规划：目标函数和约束函数皆为线性 2）二次规划：目标函数为二次函数，约束函数为线性 3）非线性规划：目标函数非一次或二次函数，或者约束函数不全是线性 第二章基本概念和理论基础 1.多元函数： n元函数：

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

n元线性函数：

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

n元二次函数：

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

2.多元函数的梯度：

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

几个常用梯度公式：

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

3.梯度的两个重要性质： 性质1:函数在某点的梯度不为零，则必与过该点的等值面垂直。性质2:梯度方向是函数具有最大变化率的方向。 4.函数在与其梯度正交的方向上变化率为0；成锐角的方向上是上升的；成钝角的方向上是下降的。

5.多元函数的Hesse矩阵
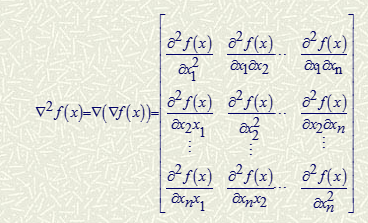
常用梯度和Hesse阵公式：

6.多元函数Taylor展开
7.多元函数的极值及判别条件 为了求出函数的局部极小值点，考察函数f 在局部极小点处满足什么条件？反过来，满足什么条件的点是局部极小点？

8.凸集：若集合D中任意两点的连线都属于D，则称D为凸集。——几何描述 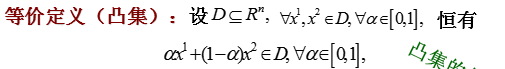——代数描述
9.凸函数： 二元：
多元：

未完待续……

Ta的文章更多 >>

《工程优化》课程总结之一
0 个评论

热门文章