P3811 【模板】乘法逆元
一行n,p 输出格式:
n行,第i行表示i在模p意义下的逆元。
10 13 输出样例#1:
1 7 9 10 8 11 2 5 3 4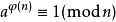 当gcd(a,n)==1 时 我们有 Aφ(n-1)≡ 1(mod n) ;
所以 我们有 A*Aφ(n-2) ≡ 1(mod n)
所以Aφ(n-2) 就是A关于mod n的逆元
当gcd(a,n)==1 时 我们有 Aφ(n-1)≡ 1(mod n) ;
所以 我们有 A*Aφ(n-2) ≡ 1(mod n)
所以Aφ(n-2) 就是A关于mod n的逆元
 1 /*
2 p为素数时 可用费马小定理
3 longlong*longlong 要慢一点 66分
4 */
5 #include
1 /*
2 p为素数时 可用费马小定理
3 longlong*longlong 要慢一点 66分
4 */
5 #include
6 #include
7
8 typedef long long LL;
9
10 int n,p;
11
12 inline LL quick_pow(LL a,int k) {
13 LL ret=1;
14 while(k) {
15 if(k&1) ret=(ret*a)%p;
16 k>>=1;
17 a=(a*a)%p;
18 }
19 return ret;
20 }
21
22 int hh() {
23 scanf("%d%d",&n,&p);
24 printf("1
");
25 for(int i=2;i<=n;++i) {
26 LL t=quick_pow(i,p-2);
27 printf("%d
",(t+p)%p);
28 }
29 return 0;
30 }
31
32 int sb=hh();
33 int main(int argc,char**argv) {;}
费马小定理
还有我们可以用exgcd来求逆元
我们知道 若ax≡1(mod p) 这我们可以写成 ax=py+1;
移项则有 ax-by=1 这明显就是扩展欧几里得
当 ax+by=gcd(a,b) gcd(a,b) == gcd(b,a%b)
我们得到 bx1+(a-a/b)y1=gcd(b,a%b);
则 ax+by=bx1+(a-(a/b)*b)y1 //这里 / 代表整除
ax+by=bx1+ay1-b*(a/b)y1
ax+by=ay1+b(x1-(a/b)*y1)
我们得到 x=y1
y=x1-(a/b)*y1;
x 即为我们所求的逆元
由于 x 可能为负数 要(x+p)%p
 1 /*
2 EXgcd 求逆元
3 比费马小定理要快一点 83分
4 */
5 #include
1 /*
2 EXgcd 求逆元
3 比费马小定理要快一点 83分
4 */
5 #include
6 #include
7
8 int n,p;
9
10 inline int exgcd(int a,int b,int&x,int&y) {
11 if(!b) {
12 x=1;y=0;
13 return a;
14 }
15 int p=exgcd(b,a%b,x,y);
16 int t=x;
17 x=y;
18 y=t-(a/b)*y;
19 return p;
20 }
21
22 int hh() {
23 scanf("%d%d",&n,&p);
24 printf("1
");
25 int x,y;
26 for(int i=2;i<=n;++i) {
27 exgcd(i,p,x,y);
28 printf("%d
",(x+p)%p);
29 }
30 return 0;
31 }
32
33 int sb=hh();
34 int main(int argc,char**argv) {;}
EXgcd
但是对于 这个题来讲 复杂度还是不够
我们还有线性求逆元的方法
来看带余除法 式子 p=k*i+r
我们可以写成 k*i+r≡0(mod p)
式子两边同乘 i-1*r-1 (i-1,r-1皆为模p意义下的逆元)
所以我们有 k*r-1+i-1≡0(mod p)
i-1≡-k*r-1(mod p)
i-1≡-(p/i)*(p%i)-1(mod p)
这样我们就线性求得了逆元
 1 #include
1 #include
2 #include
3
4 typedef long long LL;
5 const int MAXN=3000010;
6
7 int n,p;
8
9 LL inv[MAXN];
10
11 int hh() {
12 scanf("%d%d",&n,&p);
13 printf("1
");
14 inv[1]=1;
15 for(int i=2;i<=n;++i) {
16 inv[i]=(LL)(p-p/i)*inv[p%i]%p;
17 printf("%d
",inv[i]);
18 }
19 return 0;
20 }
21
22 int sb=hh();
23 int main(int argc,char**argv) {;}
线性求逆元
题目背景
这是一道模板题题目描述
给定n,p求1~n中所有整数在模p意义下的乘法逆元。输入输出格式
输入格式:一行n,p 输出格式:
n行,第i行表示i在模p意义下的逆元。
输入输出样例
输入样例#1:10 13 输出样例#1:
1 7 9 10 8 11 2 5 3 4
说明
1≤n≤3×106,n<p<20000528 输入保证 p 为质数。 我们有三种办法求逆元 由欧拉定理可知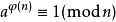 当gcd(a,n)==1 时 我们有 Aφ(n-1)≡ 1(mod n) ;
所以 我们有 A*Aφ(n-2) ≡ 1(mod n)
所以Aφ(n-2) 就是A关于mod n的逆元
当gcd(a,n)==1 时 我们有 Aφ(n-1)≡ 1(mod n) ;
所以 我们有 A*Aφ(n-2) ≡ 1(mod n)
所以Aφ(n-2) 就是A关于mod n的逆元
 1 /*
2 p为素数时 可用费马小定理
3 longlong*longlong 要慢一点 66分
4 */
5 #include
1 /*
2 p为素数时 可用费马小定理
3 longlong*longlong 要慢一点 66分
4 */
5 #include  1 /*
2 EXgcd 求逆元
3 比费马小定理要快一点 83分
4 */
5 #include
1 /*
2 EXgcd 求逆元
3 比费马小定理要快一点 83分
4 */
5 #include  1 #include
1 #include 