通信原理教程chapter4

感冒+繁忙著 教材用的是《通信原理教程》(第三版)–樊昌信著 第四章 模拟信号的数字化

文章目录

• 通信原理教程chapter4
• 抽样
• 低通模拟信号的抽样
• 带通抽样定理
• 量化
• 均匀量化
• 非均匀量化
• 编码
• 脉冲编码调制(PCM)
• 自然二进制码和折叠二进制码
• 编码方式
• 量化噪声
• 增量调制
• 增量调制的量噪比
• 结语

---

模拟信号的数字化(AD转换) 模电里面也说过,AD转换包括三个基本步骤:抽样,量化,编码,前两个在模电和信号与系统里面其实已经讲得7788了,这章的重点在于基带信号的编码.还有一些就是带通信号的抽样频率,抽样信号的非均匀量化这两个新一点的东西. 这里我们顺便帮大家复习一下信号的分类,当初看见这个图的时候,对在写的这篇blog帮助很大.务必看到每个过程中的信号是连续还是离散的

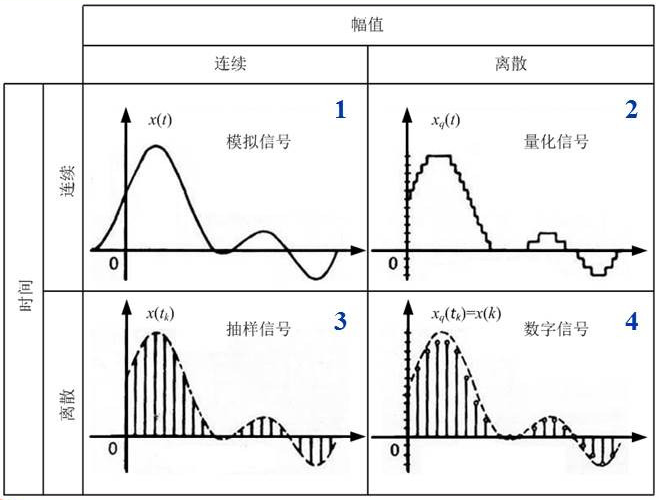
抽样

低通模拟信号的抽样

就是信号与系统学的抽样定理:
$2f_H leq f_s$
其中,$f_s$被称为奈奎斯特(Nyquist)抽样速率,当$f_s$低于$2f_H$时,重建的信号会产生混叠失真.相关的证明可自行翻阅任意一本信号与系统教材.

带通抽样定理

当我们的输入信号为一个带通信号时,显然此时的抽样频率应与信号带宽有关,而不是简单粗暴地取上限频率的两倍,这里贴一个小教程: 先从低频信号开始讲起:

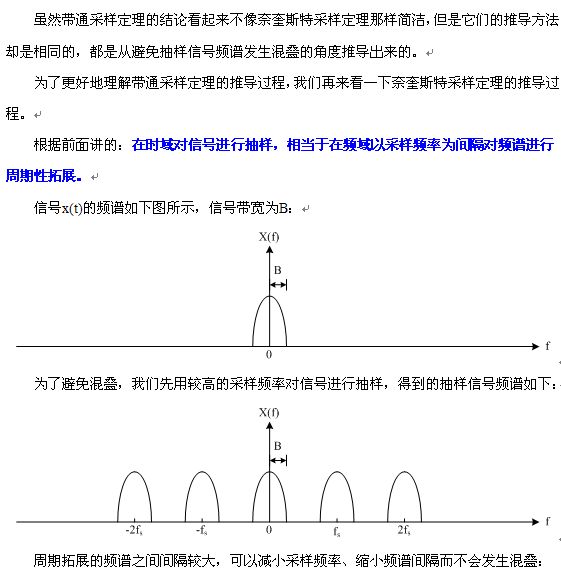
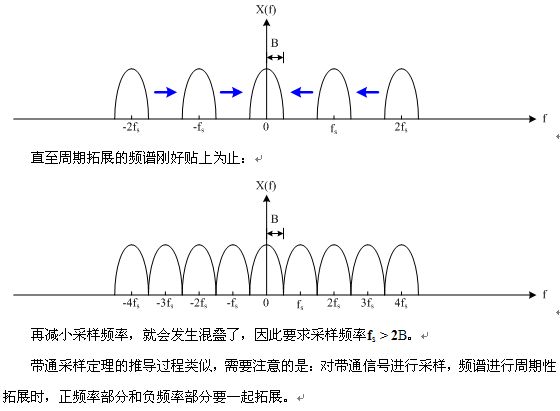
在带通采样定理中,如果要将基带信号无失真重建,我们有(和教材稍稍有不同):
$frac{2f_H}{m} leq f_s leq frac{2f_L}{m-1}$ 所以下半部分的教程是:
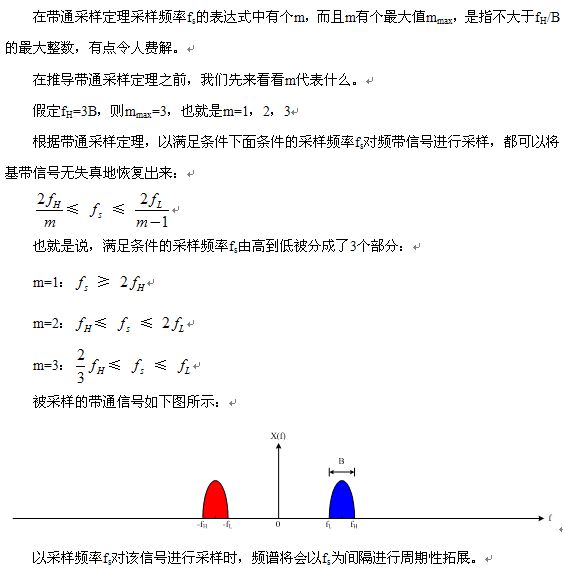
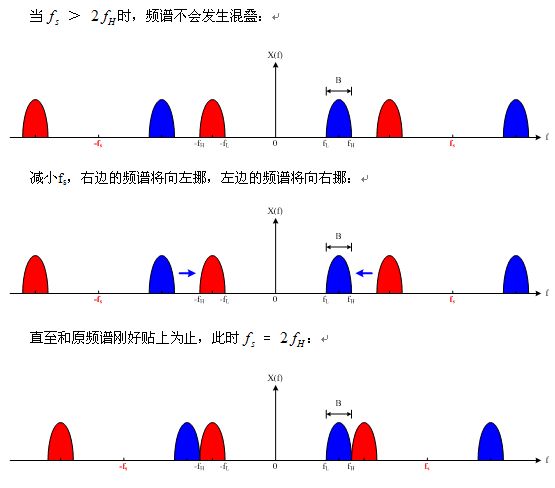
在此基础上我们来推导一下定理和书上写的公式的不同:
书上写的是:
$fs = 2B + frac{2kB}{n} = 2B(1+frac k n)$
其中B为信号带宽,
$n = lfloor frac {f_H}{B} floor quad , quad 0<k<1$
书上考虑的是信号恰好不发生混叠的时候,就是定理两个等号取到的时候,下面分两种情况来证明:

1. 上限频率是带宽的整数倍$f_H = nB$
   此时我们已知的条件有:
   $f_H = nB quad ,quad f_L=(n-1)B$
   只需回代定义式即可得:
   $f_s = 2B$
2. 上限频率不是带宽的整数倍$f_H = nB + kB quad , quad 0<k<1$
   此时我们已知的条件有:
   $f_H = nB(1 + frac k n) quad ,quad f_L=f_H -B$
   同理带回公式可得:
   $f_s = 2B(1 + frac k n)$

所以我们可以把第一种情况并入到第二种情况,即k=0,所以有:
$f_s = 2B(1 + frac k n) quad ,quad 0leq k <1$ 在计算的时候,由于k也是一个变量,所以我们只需要联立:
$egin{cases} f_s = 2B(1 + frac k n) \ f_H = nB(1+frac k n) \ n = lfloor frac {f_H}{B} floor end{cases}$
即可算出$f_s$

量化

看第一张图,这个时候是讲幅值离散化.

均匀量化

这个概念大家应该都懂,这里介绍一下他的量化误差和相应的量噪比 考虑量化电平的间隔,设取值范围为(a,b),量化电平数为M,则有量化间隔:
$riangle v = (b-a)/M$
不妨取取值范围为(-a,a),量化电平为M位,考虑其量化误差:
$N_q = E[(s_k - s_q)^2] = int^a_{-a}f(s_k)ds_k =sum^M_{i=1}int^{m_i}_{m_i-1} (s_k - s_q)^2f(s_k)ds_k$