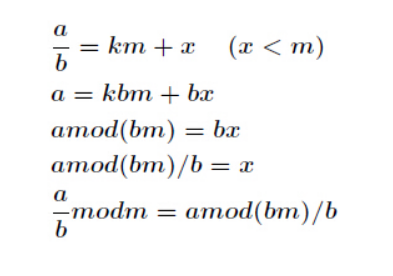class="markdown_views prism-atelier-sulphurpool-light">
我们都知道模就是余数,比如12%5=12-52=2,18%4=18-44=2。(/是程序运算中的除)
那么即把y写成+的形式就是 ,为方便理解下面我们把p写成b就是。就表示x是a的模b乘法逆元,y是b的模a乘法逆元。然后就可以用扩展欧几里得求了。
在模为素数p的情况下,有费马小定理
a^(p-1)=1(mod p)
那么a(p-2)=a-1(mod p)
也就是说a的逆元为a^(p-2)
当模p不是素数的时候需要用到欧拉
a^phi§≡1 (mod p)
a*a^(phi§-1)≡1 (mod p)
也就是说a的逆元为a^(phi§-1)
4.线性时间内求逆元(打表)
求1, 2,⋯,p−1 mod p 的逆元 (p必须为素数)

于是就可以从前面推出当前的逆元了,代码也就一行
已知

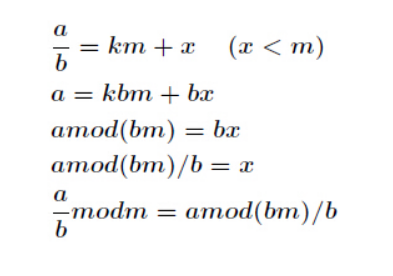
乘法逆元1.用扩展欧几里得求得逆元(a,p)=1
如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p的乘法逆元为x。
我们都知道模就是余数,比如12%5=12-52=2,18%4=18-44=2。(/是程序运算中的除)
那么即把y写成+的形式就是 ,为方便理解下面我们把p写成b就是。就表示x是a的模b乘法逆元,y是b的模a乘法逆元。然后就可以用扩展欧几里得求了。
ll exgcd(ll a,ll b,ll &x,ll &y){
if(a%b==0){
x=0ll;y=1ll;
return b;
}
ll v,tx,ty;
v=exgcd(b,a%b,tx,ty);
x=ty;
y=tx-a/b*ty;
return v;
}
ll inv(ll a,ll p){
if(!a) return 0ll;
ll x,y;
exgcd(a,p,x,y);
x=(x%p+p)%p;
return x;
}
2.用费马小定理来求逆元(a,p)=1且p为素数在模为素数p的情况下,有费马小定理
a^(p-1)=1(mod p)
那么a(p-2)=a-1(mod p)
也就是说a的逆元为a^(p-2)
ll quick_pow(ll a,ll b,ll mod){
ll ans=1;
while(b)
{
if(b&1) ans=(ans*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return ans;
}
ll inv(ll x,ll mod){
return quick_pow(x,mod-2,mod);
}
3.欧拉定理(a,p互质)当模p不是素数的时候需要用到欧拉
a^phi§≡1 (mod p)
a*a^(phi§-1)≡1 (mod p)
也就是说a的逆元为a^(phi§-1)
4.线性时间内求逆元(打表)
求1, 2,⋯,p−1 mod p 的逆元 (p必须为素数)

于是就可以从前面推出当前的逆元了,代码也就一行
A[i] = ( p - p / i) * A[p % i] % p;
5.还有一种求逆元的方法:已知