幂模运算

2019-04-13 16:06发布

站内文章 / 模拟电子
16715 0 1735
在众多的加密算法中都需要进行幂的取模运算，比如在RSA算法中需要计算ne mod N，我们称之为幂模算法。 我经常第一个想到的算法就是用pow()，最后发现根本得不到想要的结果，测试才方向是因为溢出。 当指数很大时我们采用两种方法。

方法一

利用性质：a*b%m=a*(b%m)%m a^b%m=(a%m)^b%m int mod(int a,int b,int m){ int result = 1; for(int i=0;i但当b很大时这个方法循环的次数还是相对太大，不是很理想。

方法二

进一步研究指数b的二进制表示发现，对任意的整数b都可表示为：
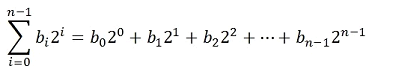
  • n表示b的实际二进制位数
  • bi表示该位是0或1
因此，ab可表示为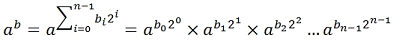： 即用b的每一位表示a的每一项，而对任意相邻的两项存在平方关系，即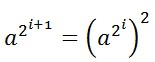： 因此我们构造下面的算法：
  • 把b转换为二进制表示，并从右至左扫描其每一位（从低到高）
  • 当扫描到第i位时，根据计算a的第i项的模，这里先是假设多有的bi都是1，记录下来，当真正的bi为1时供result使用

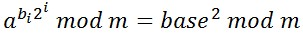
    base变量表示第i-1位时计算出的模。
  • 如果第i位为1，即bi=1,则表示该位需要参与模运算，计算结果 result = (result*base) mod m;其中result为前i-1次的计算结果。
int mod(int a,int b,int m){ int result = 1; int base = a; while(b>0){ if(b & 1==1){//与1按位与 result = (result*base) % m; } base = (base*base) %m;//难点在这 b>>=1;//相当于除2 } return result; }把时间复杂度降到了lgb，大大优于方法一。


其实还需要考虑m为负数的情况
leetcode  50. Pow(x, n) Implement pow(x, n).
为什么new要用unsigned long long？因为n可能是INT_MIN class Solution { public: double myPow(double x, int n) { double res = 1; unsigned int newn = n; if (n < 0) { x = 1 / x; newn = -n; } while (newn){ if (newn & 1){ res *= x; } x *= x; newn >>= 1; } return res; } };





热门文章