平方乘算法是快速幂的其中一种，是用于快速计算ak的方法，可以用递归的快速幂实现，其原理在于处理二进制的顺序为从高位到地位，杂度为log2(k) 基本原理：
ak,将k表示为二进制形式则得到abk...b2b1b0，其中bk为高位，b0为低位。
将abk...b2b1b0变形得到ab...bb1b02k,或者ab...bbk−1bkk−20
观察发现
bk为1时abk对答案有“加成”
bk为0时abk“不影响”答案

平方-乘算法原理

利用ab...bb1b02k（高位到低位）的顺序降幂
对于每一次的降幂
1.将当前答案平方（还原二进制位数）
2.若bk=1，则累乘基数a

非递归快速幂

利用ab...bbk−1bkk−20（低位到高位）的顺序降幂
对于每一次的降幂
1.若bk=1，则累乘当前的a
2.将当前a平方（构造当前a2k） 举个例子
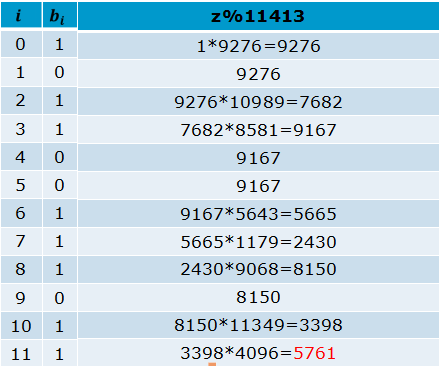
计算97263533mod11413
3533=（101100111011）2
平方乘算法（递归快速幂）
非递归快速幂