{var%20f='http://v.t.sina.com.cn/share/share.php?appkey=1515056452',u=z||d.location,p=['&url=',e(u),'&title=',e(t||d.title),'&source=',e(r),'&sourceUrl=',e(l),'&content=',c||'gb2312','&pic=',e(p||'')].join('');function%20a(){if(!window.open([f,p].join(''),'mb',['toolbar=0,status=0,resizable=1,width=440,height=430,left=',(s.width-440)/2,',top=',(s.height-430)/2].join('')))u.href=[f,p].join('');};if(/Firefox/.test(navigator.userAgent))setTimeout(a,0);else%20a();})(screen,document,encodeURIComponent,'','','https://www.xiaopingtou.cn//data/attach/topic/topicKPo7gB.jpg', '推荐 mars4zhu 的文章《CRC校验原理（cyclic redundancy check）》','https://www.xiaopingtou.net/article-53379.html','页面编码gb2312|utf-8默认gb2312'));){kind=link}
1、CRC基于“模二运算”。
模二运算类似于普通二进制运算，但是区别在于无进位和借位。
例如： 加法：010+110=100 减法：010-110=100 无进位和借位使得模二运算的加减法相当于异或操作。
乘法： 1010 * 101 ———— 1010 0000 1010 ———— 100010
除法：![]()
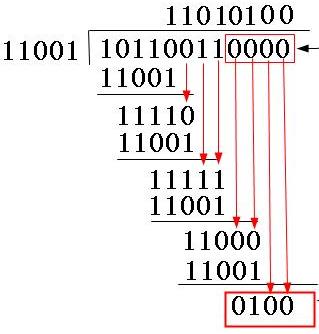
看的出来，模二运算的乘除也和普通二进制的乘除类似，唯一差别就是无进位借位（除法样例中的余数前面多的那个0可以不用管，看了下面就知道了）
2、CRC校验流程 1）选定一个除数（术语叫生成多项式），假设这个除数二进制为k位。 2）原码左移k-1位得到一个新码，比如原码1001，k为4，那么移位后就变成1001000。 3）新码模二除以这个除数，得到一个k-1位的余数（校验码）。如果余数不满k-1位，就手动在前面用0补满，比如如果余1，那就补成001。 4）把新码加上这个校验码得到CRC码，比如按以上样例，最终的CRC码就是1001001。 5）发送 6）接收之后用这个CRC码除以之前选择的除数，余数为0则传输没有出错。否则根据余数和生成多项式的一些运算（书上写的简直一堆crap，看不懂），可以得到出错位。
（图片来自http://blog.csdn.net/lycb_gz/article/details/8201987）
例如： 加法：010+110=100 减法：010-110=100 无进位和借位使得模二运算的加减法相当于异或操作。
乘法： 1010 * 101 ———— 1010 0000 1010 ———— 100010
除法：
看的出来，模二运算的乘除也和普通二进制的乘除类似，唯一差别就是无进位借位（除法样例中的余数前面多的那个0可以不用管，看了下面就知道了）
2、CRC校验流程 1）选定一个除数（术语叫生成多项式），假设这个除数二进制为k位。 2）原码左移k-1位得到一个新码，比如原码1001，k为4，那么移位后就变成1001000。 3）新码模二除以这个除数，得到一个k-1位的余数（校验码）。如果余数不满k-1位，就手动在前面用0补满，比如如果余1，那就补成001。 4）把新码加上这个校验码得到CRC码，比如按以上样例，最终的CRC码就是1001001。 5）发送 6）接收之后用这个CRC码除以之前选择的除数，余数为0则传输没有出错。否则根据余数和生成多项式的一些运算（书上写的简直一堆crap，看不懂），可以得到出错位。
（图片来自http://blog.csdn.net/lycb_gz/article/details/8201987）