今天将来学习如何求广义Fibonacci数列的循环节。
问题:给定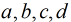 ,满足
,满足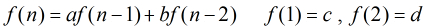 ,求
,求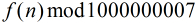 的循
环节长度。
来源:http://acdreamoj.sinaapp.com/ 1075题
分析:我们知道矩阵的递推关系如下
的循
环节长度。
来源:http://acdreamoj.sinaapp.com/ 1075题
分析:我们知道矩阵的递推关系如下
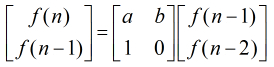 然后继续有
然后继续有
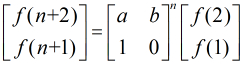 那么,现在的问题就转化为求最小的
那么,现在的问题就转化为求最小的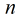 ,使得
,使得
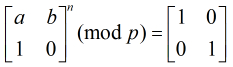 所以我们可以先找出符合条件的一个
所以我们可以先找出符合条件的一个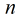 ,然后枚举它的因子,找最小的。设
,然后枚举它的因子,找最小的。设
 为了好解决问题,我们需要对矩阵
为了好解决问题,我们需要对矩阵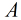 进行相似对角化,即
进行相似对角化,即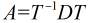 ,我们先来求
,我们先来求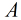 的特征值。
的特征值。
 解得
解得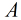 的特征值为
的特征值为
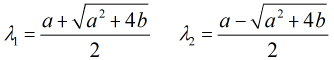 也就是说
也就是说 的相似对角矩阵
的相似对角矩阵 为
为
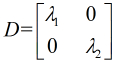 因为我们知道
因为我们知道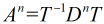 ,所以当
,所以当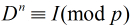 时,
时,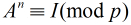 , 由于
, 由于
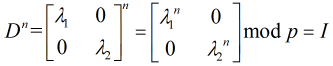 继续得到
继续得到
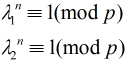 设
设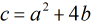 ,那么分情况讨论:
(1)
,那么分情况讨论:
(1)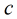 是模
是模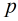 的二次剩余,由费马小定理得
的二次剩余,由费马小定理得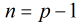 时,
时,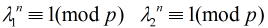 (2)
(2)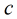 是模
是模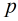 的二次非剩余,则有
的二次非剩余,则有
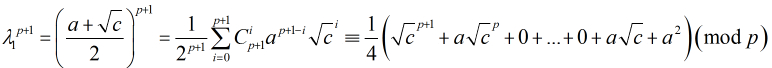 根据欧拉准则有
根据欧拉准则有
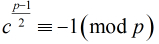 那么继续得到
那么继续得到
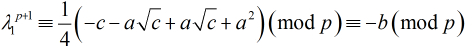 然后由费马小定理有
然后由费马小定理有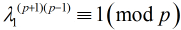 ,同理有
,同理有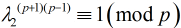 所以,当
所以,当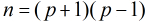 时,
时,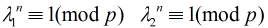 (3)
(3)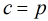 时,由于
时,由于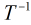 不存在,所以无法完成相似对角化,好在
不存在,所以无法完成相似对角化,好在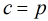 这种情况不存在。
所以综上所述:
这种情况不存在。
所以综上所述:
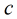 是模
是模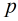 的二次剩余时,枚举
的二次剩余时,枚举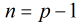 的因子
的因子
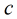 是模
是模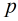 的二次非剩余时,枚举
的二次非剩余时,枚举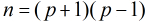 的因子
找最小的因子
的因子
找最小的因子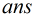 ,使得
,使得
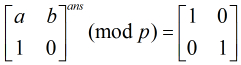 成立。
代码:
成立。
代码:
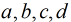 ,满足
,满足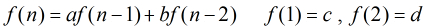 ,求
,求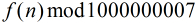 的循
环节长度。
来源:http://acdreamoj.sinaapp.com/ 1075题
分析:我们知道矩阵的递推关系如下
的循
环节长度。
来源:http://acdreamoj.sinaapp.com/ 1075题
分析:我们知道矩阵的递推关系如下
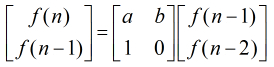 然后继续有
然后继续有
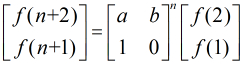 那么,现在的问题就转化为求最小的
那么,现在的问题就转化为求最小的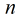 ,使得
,使得
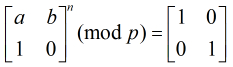 所以我们可以先找出符合条件的一个
所以我们可以先找出符合条件的一个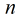 ,然后枚举它的因子,找最小的。设
,然后枚举它的因子,找最小的。设
 为了好解决问题,我们需要对矩阵
为了好解决问题,我们需要对矩阵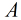 进行相似对角化,即
进行相似对角化,即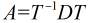 ,我们先来求
,我们先来求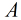 的特征值。
的特征值。
 解得
解得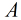 的特征值为
的特征值为
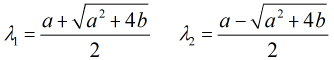 也就是说
也就是说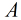 的相似对角矩阵
的相似对角矩阵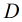 为
为
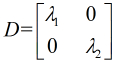 因为我们知道
因为我们知道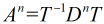 ,所以当
,所以当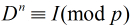 时,
时,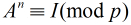 , 由于
, 由于
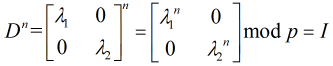 继续得到
继续得到
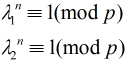 设
设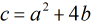 ,那么分情况讨论:
(1)
,那么分情况讨论:
(1)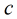 是模
是模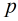 的二次剩余,由费马小定理得
的二次剩余,由费马小定理得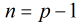 时,
时,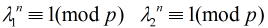 (2)
(2)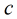 是模
是模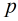 的二次非剩余,则有
的二次非剩余,则有
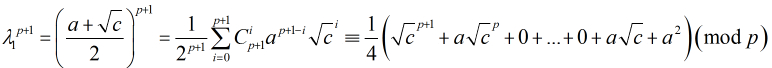 根据欧拉准则有
根据欧拉准则有
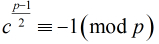 那么继续得到
那么继续得到
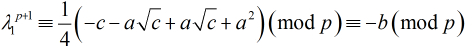 然后由费马小定理有
然后由费马小定理有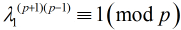 ,同理有
,同理有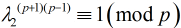 所以,当
所以,当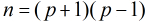 时,
时,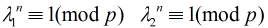 (3)
(3)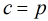 时,由于
时,由于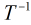 不存在,所以无法完成相似对角化,好在
不存在,所以无法完成相似对角化,好在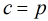 这种情况不存在。
所以综上所述:
这种情况不存在。
所以综上所述:
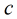 是模
是模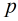 的二次剩余时,枚举
的二次剩余时,枚举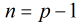 的因子
的因子
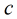 是模
是模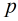 的二次非剩余时,枚举
的二次非剩余时,枚举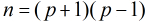 的因子
找最小的因子
的因子
找最小的因子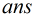 ,使得
,使得
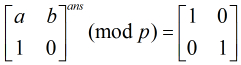 成立。
代码:
成立。
代码:
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 2;
const LL MOD = 1000000007;
LL fac[2][505];
int cnt,ct;
LL pri[6] = {2, 3, 7, 109, 167, 500000003};
LL num[6] = {4, 2, 1, 2, 1, 1};
struct Matrix
{
LL m[N][N];
} ;
Matrix A;
Matrix I = {1, 0, 0, 1};
Matrix multi(Matrix a,Matrix b)
{
Matrix c;
for(int i=0; i>= 1;
p = multi(p,p);
}
return ans;
}
LL quick_mod(LL a,LL b)
{
LL ans = 1;
a %= MOD;
while(b)
{
if(b & 1)
{
ans = ans * a % MOD;
b--;
}
b >>= 1;
a = a * a % MOD;
}
return ans;
}
LL Legendre(LL a,LL p)
{
LL t = quick_mod(a,(p-1)>>1);
if(t == 1) return 1;
return -1;
}
void dfs(int dept,LL product = 1)
{
if(dept == cnt)
{
fac[1][ct++] = product;
return;
}
for(int i=0; i<=num[dept]; i++)
{
dfs(dept+1,product);
product *= pri[dept];
}
}
bool OK(Matrix A,LL n)
{
Matrix ans = power(A,n);
return ans.m[0][0] == 1 && ans.m[0][1] == 0 &&
ans.m[1][0] == 0 && ans.m[1][1] == 1;
}
int main()
{
fac[0][0] = 1;
fac[0][1] = 2;
fac[0][2] = 500000003;
fac[0][3] = 1000000006;
LL a,b,c,d;
while(cin>>a>>b>>c>>d)
{
LL t = a * a + 4 * b;
A.m[0][0] = a;
A.m[0][1] = b;
A.m[1][0] = 1;
A.m[1][1] = 0;
if(Legendre(t,MOD) == 1)
{
for(int i=0; i<4; i++)
{
if(OK(A,fac[0][i]))
{
cout<