逆元定义:对于正整数 和
和 ,如果有
,如果有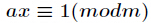 ,那么把这个同余方程中
,那么把这个同余方程中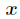 的最小正整数解叫做
的最小正整数解叫做 模
模 的逆元。
一般用欧几里得扩展来做:ax+by=1;称a和b互为逆元
详细扩展欧几里德算法介绍,解决该题的关键是:
1、了解扩展欧几里德算法,可以运用其解出gcd(a,b)=ax1+by1中的x1、y1的值
2、由题可得以下内容:
n=A%9973,则n=A-k*9973。设A/B=x,则A=Bx。所以Bx-k*9973=n。即Bx-9973y=n。
到这里我们可以发现:只要求出x的值,即可算出x%9973,也就是(A/B)%9973了。顺利解决了!
3、题目关键转到如何求出x了。题目的输入是n和B,利用扩展欧几里德算法可求出gcd(B,9973)=Bx1+9973y1=1的x1。
等式两边同乘以n,得B(nx1)-9973(-ny1)=n。可知nx1就是Bx-9973y=n的解了!!!即x=nx1。
4、对于第三部得到的x可能是负数,由题这显然是不正确的。
可以做这样的转化:(x%997373+9973)%9973
(最后一点也不太懂,不懂转化后为啥任然正确!期待大神赐教)//几天后来补一刀,如不这样写,会出现负数
的逆元。
一般用欧几里得扩展来做:ax+by=1;称a和b互为逆元
详细扩展欧几里德算法介绍,解决该题的关键是:
1、了解扩展欧几里德算法,可以运用其解出gcd(a,b)=ax1+by1中的x1、y1的值
2、由题可得以下内容:
n=A%9973,则n=A-k*9973。设A/B=x,则A=Bx。所以Bx-k*9973=n。即Bx-9973y=n。
到这里我们可以发现:只要求出x的值,即可算出x%9973,也就是(A/B)%9973了。顺利解决了!
3、题目关键转到如何求出x了。题目的输入是n和B,利用扩展欧几里德算法可求出gcd(B,9973)=Bx1+9973y1=1的x1。
等式两边同乘以n,得B(nx1)-9973(-ny1)=n。可知nx1就是Bx-9973y=n的解了!!!即x=nx1。
4、对于第三部得到的x可能是负数,由题这显然是不正确的。
可以做这样的转化:(x%997373+9973)%9973
(最后一点也不太懂,不懂转化后为啥任然正确!期待大神赐教)//几天后来补一刀,如不这样写,会出现负数
 和
和 ,如果有
,如果有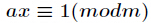 ,那么把这个同余方程中
,那么把这个同余方程中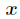 的最小正整数解叫做
的最小正整数解叫做 模
模 的逆元。
一般用欧几里得扩展来做:ax+by=1;称a和b互为逆元
详细扩展欧几里德算法介绍,解决该题的关键是:
1、了解扩展欧几里德算法,可以运用其解出gcd(a,b)=ax1+by1中的x1、y1的值
2、由题可得以下内容:
n=A%9973,则n=A-k*9973。设A/B=x,则A=Bx。所以Bx-k*9973=n。即Bx-9973y=n。
到这里我们可以发现:只要求出x的值,即可算出x%9973,也就是(A/B)%9973了。顺利解决了!
3、题目关键转到如何求出x了。题目的输入是n和B,利用扩展欧几里德算法可求出gcd(B,9973)=Bx1+9973y1=1的x1。
等式两边同乘以n,得B(nx1)-9973(-ny1)=n。可知nx1就是Bx-9973y=n的解了!!!即x=nx1。
4、对于第三部得到的x可能是负数,由题这显然是不正确的。
可以做这样的转化:(x%997373+9973)%9973
(最后一点也不太懂,不懂转化后为啥任然正确!期待大神赐教)//几天后来补一刀,如不这样写,会出现负数
的逆元。
一般用欧几里得扩展来做:ax+by=1;称a和b互为逆元
详细扩展欧几里德算法介绍,解决该题的关键是:
1、了解扩展欧几里德算法,可以运用其解出gcd(a,b)=ax1+by1中的x1、y1的值
2、由题可得以下内容:
n=A%9973,则n=A-k*9973。设A/B=x,则A=Bx。所以Bx-k*9973=n。即Bx-9973y=n。
到这里我们可以发现:只要求出x的值,即可算出x%9973,也就是(A/B)%9973了。顺利解决了!
3、题目关键转到如何求出x了。题目的输入是n和B,利用扩展欧几里德算法可求出gcd(B,9973)=Bx1+9973y1=1的x1。
等式两边同乘以n,得B(nx1)-9973(-ny1)=n。可知nx1就是Bx-9973y=n的解了!!!即x=nx1。
4、对于第三部得到的x可能是负数,由题这显然是不正确的。
可以做这样的转化:(x%997373+9973)%9973
(最后一点也不太懂,不懂转化后为啥任然正确!期待大神赐教)//几天后来补一刀,如不这样写,会出现负数
#include
#include
#include
#include
#include
using namespace std;
int m=9973;
void ojilide(long long a,long long b,long long &x,long long &y)
{
if(b==0)
{
x=1;y=0;
return;
}
else
{
ojilide(b,a%b,x,y);
int tmp=x;
x=y;
y=tmp-a/b*y;
}
}
int main()
{
long long n,b,a,x,y;
int t;
scanf("%d",&t);
while(t--)
{
scanf("%lld%lld",&n,&b);
ojilide(b,m,x,y);
x=x*n;
x=(x%m+m)%m;
printf("%lld
",x);
}
}