中国剩余定理(CRT)的表述如下
设正整数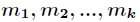 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模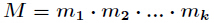 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中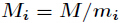 ,而
,而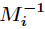 为
为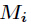 模
模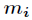 的逆元。
的逆元。
具体证明如下:
找出所有整数x,使其被3,5和7除时,余数分别为2,3和2 x≡2(mod 3)
x≡3(mod 5)=>x = △ + 3*5*7*t(△为期中的一个解,t为整数) x≡2(mod 7) 在同余中最重要的观念就是求出第一个解,那么x = △ + 3*5*7*t就是通解。那怎么求一个解呢?
利用同余的加性: 把x拆成a+b+c,即x = a + b + c 令 a≡2(mod 3) a≡0(mod 5)=>a=35p(可以看到p取1的时候满足a≡2(mod3),即a=35) a≡0(mod 7)
接下来要求b: b≡0(mod 3)
b≡3(mod 5)=>b=21q(可以看到q取3的时候满足b≡3(mod5),即b=63) b≡0(mod 7)
求c c≡0(mod 3)
c≡0(mod 5)=>c=15m(可以看到m取2的时候满足c≡2(mod7),即c=30) c≡2(mod 7)
得 x≡2(mod 3) ≡ a + b + c
x≡3(mod 5) ≡ a + b + c
x≡2(mod 7) ≡ a + b + c
a b c 都求出来之后,可以利用同余的加性 x = a + b + c = 128是一个解,x = 128 + 105t 在适当调整t之后就可以求出x在任何范围内的解,比如说求最小正整数解,这时候t取-1,得x=23
利用同余的乘性:
之前令x = a + b + c,用同余的乘性之后x = 2*a' + 3*b' + 2*c' a'≡1(mod 3) a'≡0(mod 5) =>a'=35p(可以看到p取2的时候满足a'≡1(mod3),即a'=70) a'≡0(mod 7)
接下来要求b': b'≡0(mod 3)
b'≡1(mod 5)=>b'=21q(可以看到q取1的时候满足b'≡1(mod5),即b'=21) b'≡0(mod 7)
现在来看c' c'≡0(mod 3)
c'≡0(mod 5) =>c'=15m(可以看到m取1的时候满足c'≡1(mod7),即c'=15) c'≡1(mod 7)
有了a' b' c'之后就可以得到 x = 2*a' + 3*b' + 2*c' 代入a' b' c'之后就可以得到x的一个解及其通解 x = 2*70 + 3*21 +2*15 x = 233 + 105t
在知道同余的加性和乘性之后再看下面这个公式就没有什么问题了
最后分享YouTube上关于同余加性和乘性的讲解链接 加性:https://www.youtube.com/watch?v=bFisuyRQEGk
乘性:https://www.youtube.com/watch?v=N68Yo9oyrM8
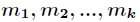 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模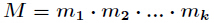 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中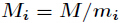 ,而
,而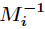 为
为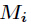 模
模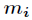 的逆元。
的逆元。
具体证明如下:
找出所有整数x,使其被3,5和7除时,余数分别为2,3和2 x≡2(mod 3)
x≡3(mod 5)=>x = △ + 3*5*7*t(△为期中的一个解,t为整数) x≡2(mod 7) 在同余中最重要的观念就是求出第一个解,那么x = △ + 3*5*7*t就是通解。那怎么求一个解呢?
利用同余的加性: 把x拆成a+b+c,即x = a + b + c 令 a≡2(mod 3) a≡0(mod 5)=>a=35p(可以看到p取1的时候满足a≡2(mod3),即a=35) a≡0(mod 7)
接下来要求b: b≡0(mod 3)
b≡3(mod 5)=>b=21q(可以看到q取3的时候满足b≡3(mod5),即b=63) b≡0(mod 7)
求c c≡0(mod 3)
c≡0(mod 5)=>c=15m(可以看到m取2的时候满足c≡2(mod7),即c=30) c≡2(mod 7)
得 x≡2(mod 3) ≡ a + b + c
x≡3(mod 5) ≡ a + b + c
x≡2(mod 7) ≡ a + b + c
a b c 都求出来之后,可以利用同余的加性 x = a + b + c = 128是一个解,x = 128 + 105t 在适当调整t之后就可以求出x在任何范围内的解,比如说求最小正整数解,这时候t取-1,得x=23
利用同余的乘性:
之前令x = a + b + c,用同余的乘性之后x = 2*a' + 3*b' + 2*c' a'≡1(mod 3) a'≡0(mod 5) =>a'=35p(可以看到p取2的时候满足a'≡1(mod3),即a'=70) a'≡0(mod 7)
接下来要求b': b'≡0(mod 3)
b'≡1(mod 5)=>b'=21q(可以看到q取1的时候满足b'≡1(mod5),即b'=21) b'≡0(mod 7)
现在来看c' c'≡0(mod 3)
c'≡0(mod 5) =>c'=15m(可以看到m取1的时候满足c'≡1(mod7),即c'=15) c'≡1(mod 7)
有了a' b' c'之后就可以得到 x = 2*a' + 3*b' + 2*c' 代入a' b' c'之后就可以得到x的一个解及其通解 x = 2*70 + 3*21 +2*15 x = 233 + 105t
在知道同余的加性和乘性之后再看下面这个公式就没有什么问题了

最后分享YouTube上关于同余加性和乘性的讲解链接 加性:https://www.youtube.com/watch?v=bFisuyRQEGk
乘性:https://www.youtube.com/watch?v=N68Yo9oyrM8