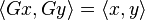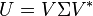若一n行n列的复数矩阵U满足
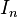 为n阶单位矩阵,
为n阶单位矩阵,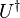 为U的共轭转置,为酉矩阵(英文:
Unitary Matrix, Unitary 是归一或单位的意思)。即,矩阵U为酉矩阵,当且仅当其共轭转置
为U的共轭转置,为酉矩阵(英文:
Unitary Matrix, Unitary 是归一或单位的意思)。即,矩阵U为酉矩阵,当且仅当其共轭转置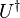 为其逆矩阵:
为其逆矩阵:
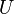 为n阶方阵,则下列条件等价:
酉矩阵的特征值都是模为1的复数,即分布在复平面的单位圆上,因此酉矩阵行列式的值也为1。
酉矩阵是正规矩阵,由谱定理知,酉矩阵U可被分解为
为n阶方阵,则下列条件等价:
酉矩阵的特征值都是模为1的复数,即分布在复平面的单位圆上,因此酉矩阵行列式的值也为1。
酉矩阵是正规矩阵,由谱定理知,酉矩阵U可被分解为
 是主对角线上元素绝对值为1的对角阵。
对任意n,所有n阶酉矩阵的集合关于矩阵乘法构成一个群。
是主对角线上元素绝对值为1的对角阵。
对任意n,所有n阶酉矩阵的集合关于矩阵乘法构成一个群。
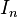 为n阶单位矩阵,
为n阶单位矩阵,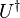 为U的共轭转置,为酉矩阵(英文:
Unitary Matrix, Unitary 是归一或单位的意思)。即,矩阵U为酉矩阵,当且仅当其共轭转置
为U的共轭转置,为酉矩阵(英文:
Unitary Matrix, Unitary 是归一或单位的意思)。即,矩阵U为酉矩阵,当且仅当其共轭转置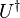 为其逆矩阵:
为其逆矩阵:
-
 。
。
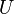 为n阶方阵,则下列条件等价:
酉矩阵的特征值都是模为1的复数,即分布在复平面的单位圆上,因此酉矩阵行列式的值也为1。
酉矩阵是正规矩阵,由谱定理知,酉矩阵U可被分解为
为n阶方阵,则下列条件等价:
酉矩阵的特征值都是模为1的复数,即分布在复平面的单位圆上,因此酉矩阵行列式的值也为1。
酉矩阵是正规矩阵,由谱定理知,酉矩阵U可被分解为
 是主对角线上元素绝对值为1的对角阵。
对任意n,所有n阶酉矩阵的集合关于矩阵乘法构成一个群。
是主对角线上元素绝对值为1的对角阵。
对任意n,所有n阶酉矩阵的集合关于矩阵乘法构成一个群。