sicily 1020. Big Interger 有数学公式

2019-04-13 17:34发布

站内文章 / 模拟电子
14497 0 1580
//大数取模，模为整型，运用到数学公式
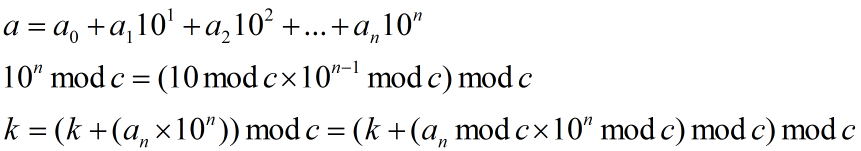
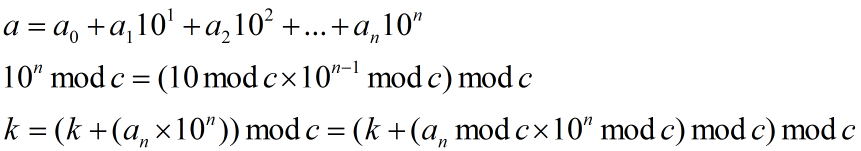
式1表示一个数，式2是关于10^n mod c 的递推公式。对于式3，赋值前，k是前面10^(n-1)数量级的和取模的结果，每步进行递推，最后即可得到结果。另外需要记录一个变量专门存储10^n mod c的值 #include #include #include using namespace std; int mod[100]; int bigIntMod(string num, int mod) { int result = (num[num.size() - 1] - '0') % mod , result10 = 1 % mod; for (int i = num.size() - 2; i >= 0; i--){ result10 = ((10 % mod) * (result10 % mod) ) % mod; result = ( result + ((num[i] - '0') % mod * (result10 % mod) ) % mod ) % mod; } return result; } int main() { int testCase; scanf("%d",&testCase); while ( testCase-- ){ int numCount; scanf("%d",&numCount); for ( int i = 0 ; i < numCount; i++){ scanf("%d",&mod[i]); } string num; cin >> num; printf("(%d",bigIntMod(num,mod[0])); for ( int i = 1 ; i < numCount; i++) printf(",%d",bigIntMod(num,mod[i])); printf(") "); } return 0; }

热门文章