Problem of Precision
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1547 Accepted Submission(s): 940
Problem Description
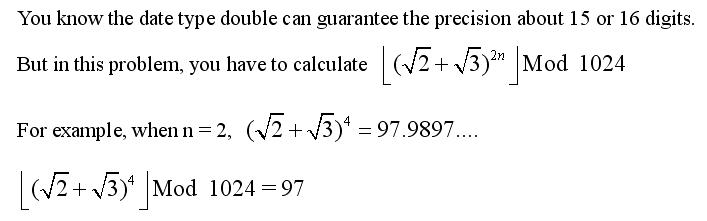
Input The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)
Output For each input case, you should output the answer in one line.
Sample Input 3 1 2 5
Sample Output 9 97 841
题意:(sqrt(2)+sqrt(3))的 2*n次方并%1024 注意:小数不能直接mod,但是如果你取整之后再mod,结果肯定出问题,因为浮点数的精度问题
题解: 推导得到递推式,构造矩阵:
 分割线以下,如果直接取模的话上面已经说了会有问题,可以自己试试
然后转化一下得到更加精确的公式,最后在取模才能得到正确的答案
分割线以下,如果直接取模的话上面已经说了会有问题,可以自己试试
然后转化一下得到更加精确的公式,最后在取模才能得到正确的答案#include
#include
#include
#include
using namespace std;
#define LL long long
#define mod 1024
LL n;
struct Matrix{
int m[15][15];
};
Matrix unit,init;
void Init()
{
init.m[0][0]=5;
init.m[0][1]=12;
init.m[1][0]=2;
init.m[1][1]=5;
memset(unit.m,0,sizeof(unit.m));
for(int i=0;i<2;i++)
unit.m[i][i]=1;
}
Matrix Mul(Matrix a,Matrix b){
Matrix c;
for(int i=0;i<10;i++)
for(int j=0;j<10;j++){
c.m[i][j]=0;
for(int k=0;k<10;k++)
c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
c.m[i][j]%=mod;
}
return c;
}
Matrix Pow(Matrix a,Matrix b,int x){
while(x)
{
if(x&1)
b=Mul(a,b);
a=Mul(a,a);
x>>=1;
}
return b;
}
int main()
{
int T;
freopen("in.txt","r",stdin);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
Init();
Matrix res=Pow(init,unit,n-1);
LL ans=5*res.m[0][0]+2*res.m[0][1];
printf("%lld
",(ans*2-1)%mod);
}
return 0;
}