指数分布族须满足这个公式形式:  其中
其中  叫自然参数,一般是一个实数,
叫自然参数,一般是一个实数, 叫做充分统计量,统计学里的知识,一般为等于
叫做充分统计量,统计学里的知识,一般为等于 。
当
。
当  不同时,分布就不同。
指数分布族包括很多(高斯分布,伯努利分布,泊松分布,伽马分布,指数分布等等)
下面证明伯努利分布属于指数分布族(对应逻辑斯蒂回归):
伯努利分布:
不同时,分布就不同。
指数分布族包括很多(高斯分布,伯努利分布,泊松分布,伽马分布,指数分布等等)
下面证明伯努利分布属于指数分布族(对应逻辑斯蒂回归):
伯努利分布:
 是
是 等于1的概率
等于1的概率

 对照两个式子得出:
对照两个式子得出:
 ;
;
 ;
;
 ;
; 所以伯努利分布满足指数分布族式子规范,即属于指数分布族。
且根据
所以伯努利分布满足指数分布族式子规范,即属于指数分布族。
且根据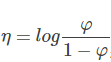 得到
得到 广义线性模型必须满足三个假设(嫌字多直接跳到我下面的解释):
广义线性模型必须满足三个假设(嫌字多直接跳到我下面的解释):
 解释下这三个假设从而推出sigmoid:
第一项,属于指数分布族,逻辑斯蒂回归满足。(因为逻辑回归假设x条件下y服从伯努利分布);
第二项,学习的输出即preY=E(T(y)|x),这里E(T(y)|x)就是x条件下y的期望,怎么计算?回忆下概率 论的知识,y是随机变量, 取值为{0,1},概率 p(y=1)=
解释下这三个假设从而推出sigmoid:
第一项,属于指数分布族,逻辑斯蒂回归满足。(因为逻辑回归假设x条件下y服从伯努利分布);
第二项,学习的输出即preY=E(T(y)|x),这里E(T(y)|x)就是x条件下y的期望,怎么计算?回忆下概率 论的知识,y是随机变量, 取值为{0,1},概率 p(y=1)= ,则期望=1* p(y=1)+0*p(y=0) =
,则期望=1* p(y=1)+0*p(y=0) =  ,所以preY=
,所以preY= ,又根据上述推导
,又根据上述推导 ,所以preY=
,所以preY= 第三项,
第三项, ,推出sigmoid函数。
好多博客说法很不规范,包括将预测的函数说成目标函数,还有推导也不清晰,所以自己总结了下,只证明逻辑回归,线性回归的话请看下面的链接。参考了此博客(这篇相对很规范也很清晰):
http://blog.csdn.net/pi9nc/article/details/12571657
转自博客:https://blog.csdn.net/shevchenkoniit/article/details/79593837
,推出sigmoid函数。
好多博客说法很不规范,包括将预测的函数说成目标函数,还有推导也不清晰,所以自己总结了下,只证明逻辑回归,线性回归的话请看下面的链接。参考了此博客(这篇相对很规范也很清晰):
http://blog.csdn.net/pi9nc/article/details/12571657
转自博客:https://blog.csdn.net/shevchenkoniit/article/details/79593837
 其中
其中  叫自然参数,一般是一个实数,
叫自然参数,一般是一个实数, 叫做充分统计量,统计学里的知识,一般为等于
叫做充分统计量,统计学里的知识,一般为等于 。
当
。
当  不同时,分布就不同。
指数分布族包括很多(高斯分布,伯努利分布,泊松分布,伽马分布,指数分布等等)
下面证明伯努利分布属于指数分布族(对应逻辑斯蒂回归):
伯努利分布:
不同时,分布就不同。
指数分布族包括很多(高斯分布,伯努利分布,泊松分布,伽马分布,指数分布等等)
下面证明伯努利分布属于指数分布族(对应逻辑斯蒂回归):
伯努利分布:
 是
是 等于1的概率
等于1的概率

 对照两个式子得出:
对照两个式子得出:
 ;
;
 ;
;
 ;
; 所以伯努利分布满足指数分布族式子规范,即属于指数分布族。
且根据
所以伯努利分布满足指数分布族式子规范,即属于指数分布族。
且根据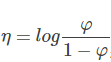 得到
得到 广义线性模型必须满足三个假设(嫌字多直接跳到我下面的解释):
广义线性模型必须满足三个假设(嫌字多直接跳到我下面的解释):
 解释下这三个假设从而推出sigmoid:
第一项,属于指数分布族,逻辑斯蒂回归满足。(因为逻辑回归假设x条件下y服从伯努利分布);
第二项,学习的输出即preY=E(T(y)|x),这里E(T(y)|x)就是x条件下y的期望,怎么计算?回忆下概率 论的知识,y是随机变量, 取值为{0,1},概率 p(y=1)=
解释下这三个假设从而推出sigmoid:
第一项,属于指数分布族,逻辑斯蒂回归满足。(因为逻辑回归假设x条件下y服从伯努利分布);
第二项,学习的输出即preY=E(T(y)|x),这里E(T(y)|x)就是x条件下y的期望,怎么计算?回忆下概率 论的知识,y是随机变量, 取值为{0,1},概率 p(y=1)= ,则期望=1* p(y=1)+0*p(y=0) =
,则期望=1* p(y=1)+0*p(y=0) =  ,所以preY=
,所以preY= ,又根据上述推导
,又根据上述推导 ,所以preY=
,所以preY= 第三项,
第三项, ,推出sigmoid函数。
好多博客说法很不规范,包括将预测的函数说成目标函数,还有推导也不清晰,所以自己总结了下,只证明逻辑回归,线性回归的话请看下面的链接。参考了此博客(这篇相对很规范也很清晰):
http://blog.csdn.net/pi9nc/article/details/12571657
转自博客:https://blog.csdn.net/shevchenkoniit/article/details/79593837
,推出sigmoid函数。
好多博客说法很不规范,包括将预测的函数说成目标函数,还有推导也不清晰,所以自己总结了下,只证明逻辑回归,线性回归的话请看下面的链接。参考了此博客(这篇相对很规范也很清晰):
http://blog.csdn.net/pi9nc/article/details/12571657
转自博客:https://blog.csdn.net/shevchenkoniit/article/details/79593837