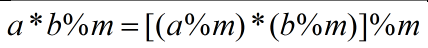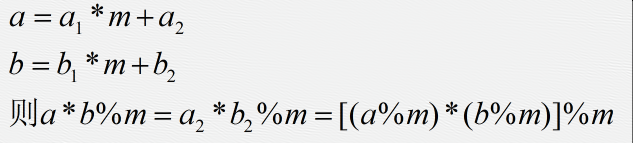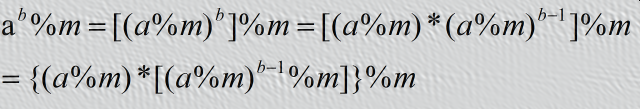快速幂与快速幂取模

2019-04-13 20:43发布

站内文章 / 模拟电子
9194 0 1076

快速幂与快速幂取模

快速幂顾名思义，就是快速算某个数的多少次幂。其时间复杂度为 O(log?N)， 与朴素的O(N)相比效率有了极大的提高。而快速幂取模就是对幂运算后结果进行取模运算。在编程过程中可能会遇到要求一个很大的数的模，为了得到一个能计算更大范围，速度更快的算法，快速幂取模算法应运而生。

快速幂

一.计算幂，计算a^b有很多种方法①有一个pow函数可以用于计算a^bpow(a,b);②利用for循环计算 int sum=1; for(int i=0;i接下来就是快速幂的各种方法。快速幂，还是很好懂的一个算法。快速幂就是把指数进行一次log(N)级别的变换
比如我们要求3^11我们可以把指数用二进制数替换11，11的二进制数也就是1011。11 = 1011=2^3+2^1+2^0而3^11就可以写成(3^8)*(3^2)*(3^1)。只需要算3^1和3^2还有3^8，这样，是不是复杂度就降了。这就是快速幂。 1,当b为偶数时，a^b可以转为a^2的b/2次方。 2.当b为奇数时，a^b可以转为a^2的b/2次方，再乘以a。   而a^2的b/2次方，以可以使用上述方式转为a^4的b/4次方再乘以某个数。我们看看代码int Quick(int a,int b) { int ans = 1,base = a; while(b!=0) { if(b%2) //如果b是奇数这两步就相当于(（a^2）^(b/2))*a ans *= base; base *= base; //这两步相当于（a^2）^(b/2) b/=2; } return ans; }在每一次进行循环时，如果b为奇数，则a^b可以转为a^2的b/2次方乘以a。所以每一次进行a^2计算时，需要根据b是否为奇数决定是否在最终的结果上乘以a。base *= base;  此步计算完成后，则base是下一个进行平方运算的数。这样当所有的循环结束后，base就是a^k，其中k是离b最近的，且为2的整数次方的数。

快速幂取模

这个也是利用了快速幂的算法，但是在写程序之前，你得知道一个知识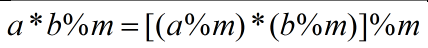
证明：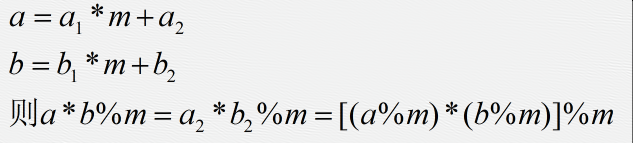
则我们计算（a^b）%m时就能得出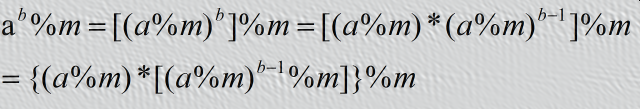
int QuickMod(int a, int b, int m) { int ans = 1; int base = a; base = base % m; while(b>0) { if(b % 2 == 1) ans = (ans * base) % m;//怕溢出如下 b = b/2; base = (base * base) % m;//如果怕溢出，那可以写成base = (base % m * base % m) % m; } return ans; }大同小异水平限制，只能写成这样了。希望能对你们学习有帮助，为你在编程之路献上绵薄之力。

热门文章