首先来看中国剩余定理：        中国剩余定理是古代求解一阶线性同余式的方法，如以下这个同余方程组求解x。                                                        中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，方程组 有解，并且通解可以用如下方式构造得到： 设 M = m1*m2*…*mn 是整数m1,m2, … ,mn的乘积，并设 Mi = M/mi 是除了mi以外的n-1个整数的乘积。 设 ti = Mi^(-1) 为 Mi 模 mi 的数论倒数(ti 为 Mi 模 mi 意义下的逆元)
Mi*ti ≡ 1(mod mi),i∈{1,2,3,…,n}
方程组 (S) 的通解形式为
x = k*M + ∑(ai*ti*Mi),i∈{1,2,3,…,n},k∈Z
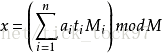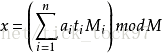在模 M 的意义下，方程组(S)只有一个解如下图所示   拓展欧几里得定理：         对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然 存在整数对 x，y ，使得 gcd（a，b）=a*x+b*y。 如何求出x，y呢？当b=0时，很容易得出一组解x=1，y=0，我们知道b*x1+a%b*y1=gcd(b,a%b)=gcd(b,a%b),b*x1+a%b*y1=b*x1+(a-a/b*b)*y1=a*y1+b*(x1-a/b*y1). 由恒等定理可知  x=y1,y=x1-a/b*y1;然后即可递归求出一组解。 附上代码实现 int exgcd(int a, int b, int &x, int &y){
    if (b == 0){
        x = 1;
        y = 0;
        return a;
    }
    int r = exgcd(b, a%b, x, y);
    int t = x;
    x=y；
    y = t - a / b*y;
    return r;
} 拓展欧几里得的应用 1、求解不定方程          对于方程a*x+b*y=c.求解x和y。gcd(a,b)为a和b的1最大公约数，若c%gcd(a,b)==0,则原方程有整数解，否则，无整数解。       对于求解方法，先用上述方法求出a*x+b*y=gcd(a,b)的一组特解x1,y1，则原方程的一组特解x2=x1*c/gcd(a,b),y2=y1*c/gcd(a,b); 原方程的通解为     x=x2+b/gcd(a,b)*k,y=y2-a/gcd(a,b)*k.其中k为任意整数。 2、求解同余方程 求解方程 ax≡b (mod n) 相当于求解方程 ax+ ny= b, (x, y为整数)   ，用上述方法求解即可。 3、求逆元    同余方程ax≡b (mod n)，如果 gcd(a,n)== 1，则方程只有唯一解。       在这种情况下，如果 b== 1，同余方程就是 ax=1 (mod n ),gcd(a,n)= 1。       这时称求出的 x 为 a 的对模 n 乘法的逆元。       对于同余方程 ax= 1(mod n )， gcd(a,n)= 1 的求解就是求解方程       ax+ ny= 1，x, y 为整数。这个可用扩展欧几里德算法求出，原同余方程的唯一解就是用扩展欧几里德算法得出的 x 。 void exgcd(LL a, LL b, LL& d, LL& x, LL& y) {
    if (!b) { d = a; x = 1; y = 0; }
    else { exgcd(b, a%b, d, y, x); y -= x*(a / b); }
}
LL inverse(LL a, LL n) { //求a对n的逆元，要求a与n互质
    LL d, x, y;
    exgcd(a, n, d, x, y);
    return d == 1 ? (x + n) % n : -1;
}