前期知识：

1.符号位：首位表示符号位，正数为0、负数为1； 2.在计算机中，负数以其正值的补码形式表示（将减法运算转换为加法运算）。 在以模为12的系统中，加9和减3效果是一样的，因此凡是减3运算，都可以用加9来代替。对“模”12而言，9和3互为补数（二者相加等于模）。所以我们可以得出一个结论，即在有模的计量系统中，减一个数等于加上它的补数，从而实现将减法运算转化为加法运算的目的。 2.1 原码   一个整数，按照绝对值大小转换成的二进制数，称为原码。       如 00000000 00000000 00000000 00000110 是 6 的原码 2.2 反码   将二进制数按位取反，所得的新二进制数称为原二进制数的反码。       如 00000000 00000000 00000000 00000110 的反码是 11111111 11111111 11111111 11111001

•  

2.3 补码   反码加1称为补码。也就是说，要得到一个数的补码，先得到反码，然后反码加上1，所得数称为补码。   所以 -6 在计算机器的表示形式为： # -6 的正值 6 的二进制： 00000000 00000000 00000000 00000110 # 取反得反码： 11111111 11111111 11111111 11111001 # +1 得补码，即 -6 在计算机中的二进制表示： 11111111 11111111 11111111 11111010  

按位与（&）

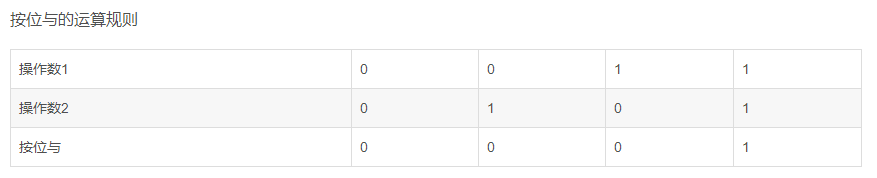
规则：两个操作数对应位同为1时，结果为1，其余全为0. （或者是只要有一个操作数为0，结果就为0） 负数的运算是以补码形式进行的，如果运算结果首位为1，结果也需要求一次补码 如何求补码？ 负数的补码得原码 补码减1取反 （更方便的一种记法是从右向左遇到第一个1为止，这个1前面的位取反，首位不动）

 按位或（|）

规则总结：只有两个操作数对应位同为0时，结果为0，其余全为1.（或者是只要有一个操作数为1，结果就为1）。

按位非（~）

规则总结：反码，取反

按位异或（^）

规则：不同为1   10^-10 为例 0000 0000 0000 0000 0000 0000 0000 1010 ^ 1111 1111 1111 1111 1111 1111 1111 0110 = 1111 1111 1111 1111 1111 1111 1111 1100 结果首位为1 再取一次补码（右向左，第一个为1的前面取反） 1000 0000 0000 0000 0000 0000 0000 0100

左位移（<<）

算术右移（>>）: 符号位不变，低位补0。如：2<<2结果为8。

 右位移（>>）

无符号右移（>>>）

低位溢出，高位补0。注意，无符号右移（>>>）中的符号位（最高位）也跟着变，无符号的意思是将符号位当作数字位看待。如：-1>>>1结果为2147483647。 参考资料：https://blog.csdn.net/leonliu06/article/details/78685248；https://blog.csdn.net/goskalrie/article/details/52796360