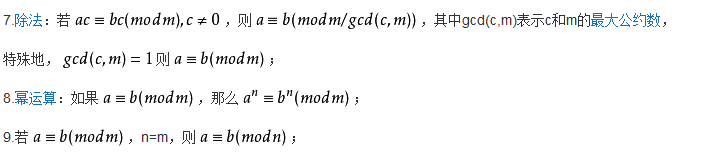同余定理
给定一个
正整数m,如果两个
整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对
模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。
记法:a≡b(mod d)
性质:反身性、对称性、传递性等
同余符号
两个整数a、b,若它们除以整数m所得的
余数相等,则称a与b对于模m同余或a同余于b模m。
记作:a≡b (mod m),
读作:a同余于b模m,或读作a与b对模m同余,例如26≡2(mod 12)。
定义
设m是大于1的正整数,a、b是整数,如果m|(a-b),则称a与b关于模m同余,记作a≡b(mod m),读作a与b对模m同余。
显然,有如下事实
(1)若a≡0(mod m),则m|a;
(2)a≡b(mod m)等价于a与b分别用m去除,余数相同。
性质
1.
反身性:a≡a (mod m);
2.
对称性:若a≡b(mod m),则b≡a (mod m);
3.传递性:若a≡b(mod m),b≡c(mod m),则a≡c(mod m);
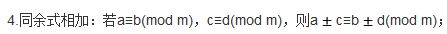
5.同余式相乘:若a≡b(mod m),c≡d(mod m),则ac≡bd(mod m)。

6.
线性运算:如果a ≡ b (mod m),c ≡ d (mod m),那么
(1)a ± c ≡ b ± d (mod m);
(2)a * c ≡ b * d (mod m)。

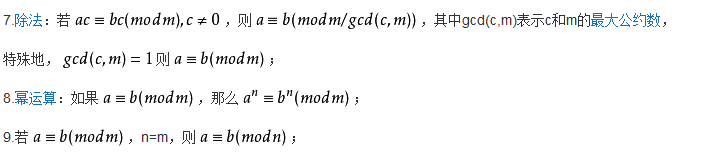

参考:
https://baike.baidu.com/item/%E5%90%8C%E4%BD%99%E5%AE%9A%E7%90%86/1212360 同余定理百度百科
 6.线性运算:如果a ≡ b (mod m),c ≡ d (mod m),那么
(1)a ± c ≡ b ± d (mod m);
(2)a * c ≡ b * d (mod m)。
6.线性运算:如果a ≡ b (mod m),c ≡ d (mod m),那么
(1)a ± c ≡ b ± d (mod m);
(2)a * c ≡ b * d (mod m)。