矩阵快速幂=矩阵乘法+快速幂
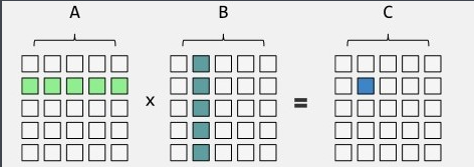
伪代码实现
F[0]=0;F[1]=1;F[2]=1;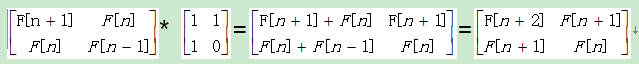
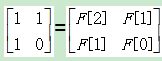
故而,此题使用矩阵快速幂取模方法
矩阵乘法

伪代码实现
Mat operator*(Mat a,Mat b) {
Mat c;
for i:0 --> len
for j:0-->len
c.mat[i][j] = 0;
for k:0-->len
c.mat[i][j]=(c.mat[i][j] + (a.mat[i][k]*b.mat[k][j])%MOD)%MOD;
return c;
}
时间复杂度O(n^3)
实数快速幂
假设你已经有一个函数F(x) = k^x 它可以求 k^1 直到 k^(n-1)分治思想
现在的问题是 如何求F(n)?
伪代码实现
- 当n是偶数的时候:F(n)=F(n/2)*F(n/2)
- 当n是奇数的时候:转化成偶数的情况 F(n) = k * F(n - 1)
/*递归写法*/
int fast_mod(int k, int n, int MOD){
n == 0:
return 1;
n是奇数:
return k * fast_mod(k, n -1, MOD) % MOD;
n是偶数:
p = fast_mod(k, n >> 1, MOD);
return p * p % MOD;
}
/*非递归写法*/
int quickmod(int a, int b){
ans = 1;
只要b不等于0:
如果b是奇数:
ans = (ans*a)%mod; b--;
如果b是偶数:
b/=2;
a = ((a%mod)*(a%mod))%mod;
return ans;
}
时间复杂度O(logN)
矩阵快速幂
伪代码实现Mat fast_mod(Mat A, int n, int MOD){
n == 0:
return E;
n是奇数:
return MulMat(A, fast_mod(A, n - 1), MOD);
n是偶数:
p = fast_mod(k, n >> 1, MOD);
return MulMat(p, p, MOD);
}
/*对于任何一个矩阵A,定义A^0 = E。E是单位矩阵*/
朴素矩阵幂运算时间复杂度是O(n^3*m),矩阵快速幂时间复杂度是O(n^3*log m)
例题:Fibonacci
poj-3070Description
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … An alternative formula for the Fibonacci sequence is.

Given an integer n, your goal is to compute the last 4 digits of Fn.
Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
Sample Input
0
9
999999999
1000000000
-1
Sample Output
0
34
626
6875
原理
F[n]=F[n-1]+F[n-2];F[0]=0;F[1]=1;F[2]=1;
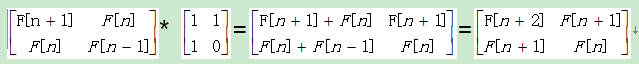
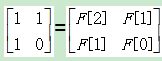
故而,此题使用矩阵快速幂取模方法
代码
/*手残党代码*/
#include
/*高效代码*/
#include