class="markdown_views prism-github-gist">
POJ 1995 Raising Modulo Numbers
原理:
比如现在要求A^156,而156(10)=10011100(2)
也就有A^156=>(A^4)(A^8)(A^16)*(A^128) 考虑到因子间的联系,我们从二进制10011100中的最右端开始
快速幂模板,最简单的 题意:
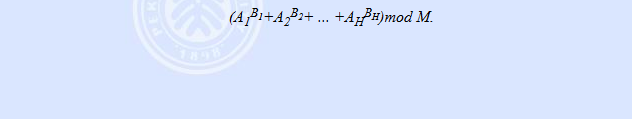 我的:对x^n进行取模运算,对n转换成x进制,然后有1的地方就要进行相乘,考虑一下位就行了
我的:对x^n进行取模运算,对n转换成x进制,然后有1的地方就要进行相乘,考虑一下位就行了
求 a * b%mod,当a和b都很大的时候:
比如现在要求A^156,而156(10)=10011100(2)
也就有A^156=>(A^4)(A^8)(A^16)*(A^128) 考虑到因子间的联系,我们从二进制10011100中的最右端开始
快速幂模板,最简单的 题意:
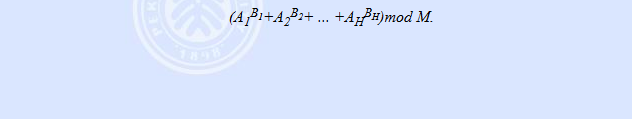 我的:对x^n进行取模运算,对n转换成x进制,然后有1的地方就要进行相乘,考虑一下位就行了
我的:对x^n进行取模运算,对n转换成x进制,然后有1的地方就要进行相乘,考虑一下位就行了
#includescanf("%lld%lld",&a[i],&b[i]);
ll ans=0;
for(int i=0;icout<return 0;
}
当取模的时候两个数相乘的时候就很大,超过long long 这个范围的时候,就得调用multi_mod函数,对两个很大的数进行拆成位然后再进行取模运算。
具体代码如下: 求 a * b%mod,当a和b都很大的时候:
ll multi_mod(ll a,ll b,ll mod_val)
{
a=a%mod_val;
b=b%mod_val;
ll ret=0;
ll t=a;
while(b)
{
if(b & 1)
{
ret =(ret+t) % mod_val;
}
b >>=1;
t = (t <<= 1) % mod_val;
}
return ret;
}