电力窃漏电用户的自动识别的笔记：
目标：
1、归纳漏电用户的关键特征，构建漏电用户的model
2、利用事实监控的数据，懂所有的用户进行实时诊断
注意的点：
1、某一些大用户不可能存在漏电行为，例如银行、学校和工商等。
2、漏电用户的窃电开始时间和结束时间是表征其漏电的关键节点，在这些节点上，用户的用电负荷和终端报警数据会有一定的变化。
样本数据抽取是务必包含一定范围的数据，并通过用户的负荷数据计算出当天的用户的用电量。 数据探索分析：
1、分布分析： 所有漏电用户的分布分析，显示每个类别的漏电用户的分布。
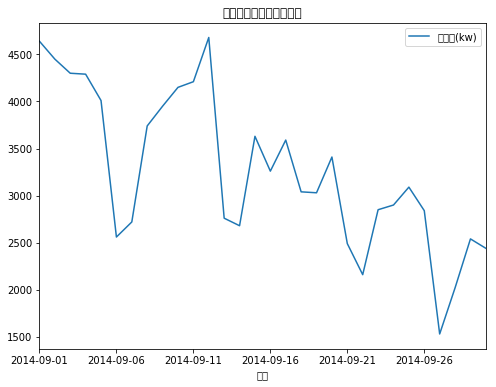
2、周期性分析：随机抽取正常用电用户额窃电用户，采用周期性分析对用电量进行探索。 #-*- conding: utf-8 -*- import pandas as pd import matplotlib.pyplot as plt import matplotlib.mlab as mlab # 正常显示中文和正负号 plt.rcParams["font.serif"] = ["SimHei"] plt.rcParams['axes.unicode_minus'] = False normalUser = pd.read_csv("data/normalUser.csv") unnormalUser = pd.read_csv("data/unnormalUser.csv") normalUser.plot(title=u"正常用电用户的电量趋势",x=normalUser["日期"],figsize=(8,6)) unnormalUser.plot(title=u"漏电用电用户的电量趋势",x=unnormalUser['日期'],figsize=(8,6)) plt.show() 数据预处理
1、数据清洗：目的是从业务和建模的相关方面考虑，筛选出需要的数据。
1、通过数据探索发现非居民用电类别中不存在漏电的现象，故将非居民类别过滤掉。
2、结合本案例，节假日用电量与工作相比，明显偏低，为了尽可能达到较好的效果，过滤掉节假日的用电数据
2、缺失值处理
1、缺失值少的情况下，一般情况下不会直接去掉数据，而是对缺失值进行填充，这里选择拉格朗日插值法进行补充。 from scipy.interpolate import lagrange #导入lagrange函数 inputfile = "data/missing_data.xls" outputfile = "data/missing_data_processed.xls" data = pd.read_excel(inputfile) # 自定义列向量差值函数 # s为列向量，n是被插值的位置，k是前后的取的个数 默认是5 def polyinterp_column(s, n, k=5): y = s[list(range(n-k,n)) + list(range(n+1,n+1+k))] y = y[y.notnull()] return lagrange(y.index, list(y))(n) for i in data.columns: for j in range(len(data)): if data[i].isnull()[j]: data[i][j] = polyinterp_column(data[i],j) data.to_excel(outputfile,header=None, index=False) 数据变换：
1、电量趋势下降指标： 用电量的趋势
考虑第i天前后5天的用电量的斜率， k[i] = sum[i-5,i+5]{(f-mean(f))(l-mean(l))} / sum[i-5,i+5]{(l-mean(j))^2}
mean(f) = 1/11 sumi-5, i+5 ; mean(l) = 1/11 sumi-5, i+5 如果用电趋势，不断下滑，则认为有窃电嫌疑，计算这11天内的，当天比前一天用电量趋势递减的天数 if(k[i] < k[i-1]) D[i] = 1 else k[i] >= k[i-1] D[i] = 0 T = sum[i-5, i+5](D[j]) 2、线损指标： 线损增长率
线损率用来衡量供电线路的损失比例，线损率是总电量s与实际用电量sum(f)的差除以总电量s。
以天为单位进行计算。
t = s / sum(f)
如果用户发生窃电，则当天的线损率会上升，用户每天用电量存在波动，以天为单文，误差较大，
所以考虑前后几天（5天）的线损率的平均值，判断增长率是否大于1%，若大于1%，则认为是窃电。
前5天的线损率平均值V[i1],后5天的平均值v[i2],若v[i1]比v[i2]的增长率大于1%，认为有窃电嫌疑。
if((v[i1] - v[i2]) / v[i2] > 1%) E[i] = 1
else E[i] = 0 3、告警类指标： 与窃电相关的终端告警数
计算发生与漏电相关的报警的总次数。 得到训练的数据。
1、进行模型的构建：
1、数据划分，0.8作为训练集，0.2作为测试集
2、LM神经网络模型：
输入节点：3
输出节点：1
隐藏节点：10
优化函数：Adam
激活函数：Relu(x)
3、CART决策树模型 # 分割数据作为训练数据和测试数据 from random import shuffle # 用来打乱数据 datafile = "data/model.xls" data = pd.read_excel(datafile) data = data.as_matrix() shuffle(data) #打乱数据 p = 0.8 #训练数据的比例 train = data[0:int(len(data)*p)] test = data[int(len(data)*p):] # 构建LM神经网络模型 from keras.models import Sequential from keras.layers import Dense, Activation modelfile = 'tmp/net.model' #存储训练好的神经网络 model = Sequential() #初始化 model.add(Dense(3,10)) # CART决策树模型 from sklearn.tree import DecisionTreeClassifier treefile = 'tmp/tree.pkl' #模型的输出的名字 tree = DecisionTreeClassifier() tree.fit(train[:,:3],train[:,3]) #保存模型,写入文件 from sklearn.externals import joblib joblib.dump(tree, treefile) 2、模型的评价
采用ROC曲线进行评估，一个优秀的分类器所对应的ROC曲线应该尽量靠近左上角。 # LM神经网络模型的ROC曲线 from sklearn.metrics import roc_curve #导入ROC曲线 predict_result = model.predict(test[:,:3].reshape(len(test))) fpr, tpr, thresholds = roc_curve(test[:,3], predict_result, pos_label=1) plt.plot(fpr,tpr,linewidth=2, label = 'ROC of LS') plt.xlabel('False Position Rate') plt.ylabel('True Position Rate') #边界范围 plt.xlim(0,1.05) plt.ylim(0,1.05) plt.legend(loc=4) plt.show() # 决策树模型的ROC曲线 from sklearn.metrics import roc_curve #导入ROC曲线 fpr, tpr, thresholds = roc_curve(test[:,3], tree.predict_proba(test[:,:3])[:,1], pos_label=1) plt.plot(fpr,tpr,linewidth=2, label = 'ROC of CART') plt.xlabel('False Position Rate') plt.ylabel('True Position Rate') #边界范围 plt.xlim(0,1.05) plt.ylim(0,1.05) plt.legend(loc=4) plt.show() normalUser.csv
https://github.com/xiaoran-2/Python_DataAnalysisAndMining/blob/master/chapter6/data/normalUser.csv unnormalUser.csv https://github.com/xiaoran-2/Python_DataAnalysisAndMining/blob/master/chapter6/data/unnormalUser.csv 配套数据:
链接: https://pan.baidu.com/s/166fcGZ1mkyW45j_1WUS-tg 提取码: wyxa