{var%20f='http://v.t.sina.com.cn/share/share.php?appkey=1515056452',u=z||d.location,p=['&url=',e(u),'&title=',e(t||d.title),'&source=',e(r),'&sourceUrl=',e(l),'&content=',c||'gb2312','&pic=',e(p||'')].join('');function%20a(){if(!window.open([f,p].join(''),'mb',['toolbar=0,status=0,resizable=1,width=440,height=430,left=',(s.width-440)/2,',top=',(s.height-430)/2].join('')))u.href=[f,p].join('');};if(/Firefox/.test(navigator.userAgent))setTimeout(a,0);else%20a();})(screen,document,encodeURIComponent,'','','https://www.xiaopingtou.cn//data/attach/topic/topicKPo7gB.jpg', '推荐 CONSON.WU 的文章《Codeforces 622F (拉格朗日插值 费马小定理)》','https://www.xiaopingtou.net/article-55453.html','页面编码gb2312|utf-8默认gb2312'));){kind=link}
做这个题之前需要知道一些知识:
拉格朗日插值:n-1次多项式可以用n个点唯一确定,插值公式是:
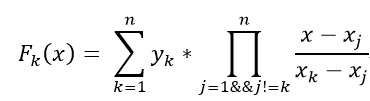
费马小定理:a^(p-1)≡1(如果p是素数),也就是说模p时a和a^(p-2)互为逆元 关于模:当p是素数时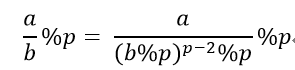
对于这道题可以发现对于每一个k次幂的积都可以用一个k+1次幂的多项式表示,于是我们可以构造出k+2个点来拟合这个多项式.拉格朗日插值公式在这里就是: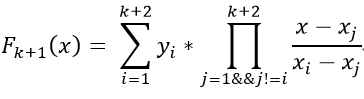
我们需要求的就是F(n),带入以后就是: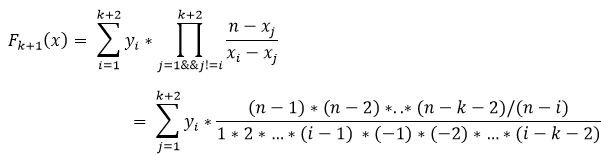
然后就是简单的预处理和取模了,仔细点就可以了
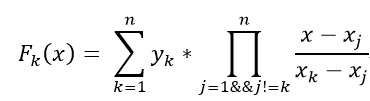
费马小定理:a^(p-1)≡1(如果p是素数),也就是说模p时a和a^(p-2)互为逆元 关于模:当p是素数时
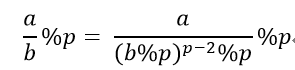
对于这道题可以发现对于每一个k次幂的积都可以用一个k+1次幂的多项式表示,于是我们可以构造出k+2个点来拟合这个多项式.拉格朗日插值公式在这里就是:
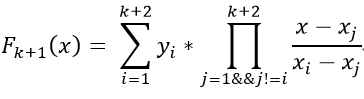
我们需要求的就是F(n),带入以后就是:
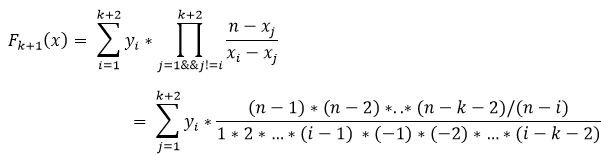
然后就是简单的预处理和取模了,仔细点就可以了
#include
using namespace std;
#define maxn 1000005
#define mod 1000000007
long long fac[maxn], y[maxn];
long long n, k;
long long qpow (long long a, long long b) {
a %= mod, b %= mod;
long long ans = 1;
while (b) {
if (b&1)
ans = ans*a%mod;
a = a*a%mod;
b >>= 1;
}
return ans;
}
int main () {
//freopen ("in.txt", "r", stdin);
cin >> n >> k;
fac[0] = 1;
for (long long i = 1; i <= k+2; i++) {
fac[i] = fac[i-1]*i%mod;
}
if (k == 0) {
cout << n << endl;
return 0;
}
y[0] = 0;
for (long long i = 1; i <= k+2; i++) {
y[i] = y[i-1]+qpow (i, k);
y[i] %= mod;
}
if (n <= k+2) {
cout << y[n] << endl;
return 0;
}
long long ans1 = 1;
for (long long i = n-k-2; i <= n-1; i++) ans1 = ans1*i%mod;
long long ans = 0;
for (long long i = 1; i <= k+2; i++) {
long long p1 = qpow (n-i, mod-2)%mod;
long long p2 = qpow (fac[i-1]*fac[k+2-i]%mod, mod-2)%mod;
long long sign = ((k+2-i)%2 == 1 ? -1 : 1);
long long cur = y[i]*p1%mod*p2%mod*ans1%mod;
cur *= sign;
if (cur < 0)
cur = (cur+mod)%mod;
ans = (ans+cur)%mod;
}
cout << ans << endl;
return 0;
}