中国剩余定理(CRT)的表述如下 设正整数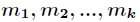 两两互素,则同余方程组
两两互素,则同余方程组  有整数解。并且在模
有整数解。并且在模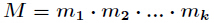 下的解是唯一的,解为
下的解是唯一的,解为  其中
其中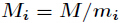 ,而
,而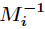 为
为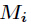 模
模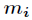 的逆元。 代码:[cpp] view plain copy
的逆元。 代码:[cpp] view plain copy

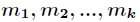 两两互素,则同余方程组
两两互素,则同余方程组  有整数解。并且在模
有整数解。并且在模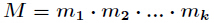 下的解是唯一的,解为
下的解是唯一的,解为  其中
其中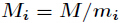 ,而
,而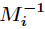 为
为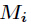 模
模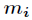 的逆元。 代码:[cpp] view plain copy
的逆元。 代码:[cpp] view plain copy - int CRT(int a[],int m[],int n)
- {
- int M = 1;
- int ans = 0;
- for(int i=1; i<=n; i++)
- M *= m[i];
- for(int i=1; i<=n; i++)
- {
- int x, y;
- int Mi = M / m[i];
- extend_Euclid(Mi, m[i], x, y);
- ans = (ans + Mi * x * a[i]) % M;
- }
- if(ans < 0) ans += M;
- return ans;
- }
详细解释
long long Rem(long long a[],long longm[],int num){
long long n1=n[0],a1=a[0],n2,a2,k1,k2,x0,gcd,c;
for(int i=1;i//解得:n1*k1+n2*k2=gcd(n1,n2)
if(c%gcd){
flag=1;
return 0;//无解
}
x0=c/gcd*k1;//n1*x0+n2*(c/gcd*k2)=c PS:k1/gcd*c错误!
t=n2/gcd;
x0=(x0%t+t)%t;//求n1*x0+n2*y=c的x0的最小解
a1+=n1*x0;
n1=n2/gcd*n1;
}
return a1;
}
long long extend_gcd(long long a,long long b,long long &x,long long &y)
{
if(a == 0 && b == 0)return -1;
if(b ==0 )
{
x = 1;
y = 0;
return a;
}
long long d = extend_gcd(b,a%b,y,x);
y -= a/b*x;
return d;
}
int m[10],a[10];//模数为m,余数为a,X % m = a
bool solve(int &m0,int &a0,int m,int a)
{
long long y,x;
int g = extend_gcd(m0,m,x,y);
if( abs(a - a0)%g )
return false;
x *= (a - a0)/g;
x %= m/g;
a0 = (x*m0 + a0);
m0 *= m/g;
a0 %= m0;
if( a0 < 0 )a0 += m0;
return true;
} /* * 无解返回false,有解返回true; * 解的形式最后为 a0 + m0 * t (0<=a0
参考资料:http://www.cnblogs.com/walker01/archive/2010/01/23/1654880.htmlhttp://blog.csdn.net/acdreamers/article/details/8050018https://www.cnblogs.com/MashiroSky/p/5918158.html