组合大发好
一般我们用杨辉三角性质
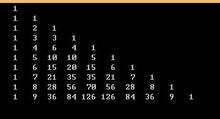
杨辉三角上的每一个数字都等于它的左上方和右上方的和(除了边界)
 第n行,第m个就是,就是C(n, m) (从0开始)
电脑上我们就开一个数组保存,像这样
第n行,第m个就是,就是C(n, m) (从0开始)
电脑上我们就开一个数组保存,像这样
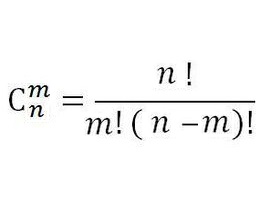 我们需要求阶乘和逆元阶乘
我们就用1e9+7来求余吧
费马小定理
a^(p-1) ≡1 (mod p)
两边同除以a
a^(p-2) ≡1/a (mod p)
数论1/a 是inv(a)
应该写a^(p-2) ≡ inv(a) (mod p)
所以inv(a) = a^(p-2) (mod p)
这个用快速幂求一下,复杂度O(logn)
引用其他人写的一句话
除法求模不能类似乘法,对于(A/B)mod C,直接(A mod C)/ (B mod C)是错误的;找到B的逆元b(b=B^-1);求出(A*b)modC即可;
由费马小定理:B 关于 P 的逆元为 B^(p-2);
费马小定理(Fermat Theory)是数论中的一个重要定理,其内容为: 假如p是质数,且gcd(a,p)=1,那么 a(p-1)≡1(mod p)。即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。所以,a^-1*a=1=a^(p-1),所以:a^-1=a^(p-2);
我们需要求阶乘和逆元阶乘
我们就用1e9+7来求余吧
费马小定理
a^(p-1) ≡1 (mod p)
两边同除以a
a^(p-2) ≡1/a (mod p)
数论1/a 是inv(a)
应该写a^(p-2) ≡ inv(a) (mod p)
所以inv(a) = a^(p-2) (mod p)
这个用快速幂求一下,复杂度O(logn)
引用其他人写的一句话
除法求模不能类似乘法,对于(A/B)mod C,直接(A mod C)/ (B mod C)是错误的;找到B的逆元b(b=B^-1);求出(A*b)modC即可;
由费马小定理:B 关于 P 的逆元为 B^(p-2);
费马小定理(Fermat Theory)是数论中的一个重要定理,其内容为: 假如p是质数,且gcd(a,p)=1,那么 a(p-1)≡1(mod p)。即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。所以,a^-1*a=1=a^(p-1),所以:a^-1=a^(p-2);
数学排列组合公式:C(n,m)= n!/(m!*(n-m)!)
 第n行,第m个就是,就是C(n, m) (从0开始)
电脑上我们就开一个数组保存,像这样
第n行,第m个就是,就是C(n, m) (从0开始)
电脑上我们就开一个数组保存,像这样

#include
const int N = 2000 + 5;
const int MOD = (int)1e9 + 7;
int comb[N][N];//comb[n][m]就是C(n,m)
void init(){
for(int i = 0; i < N; i ++){
comb[i][0] = comb[i][i] = 1;
for(int j = 1; j < i; j ++){
comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
comb[i][j] %= MOD;
}
}
}
int main(){
init();
}
(PS:大部分题目都要求求余,而且大部分都是对1e9+7这个数求余)
这种方法的复杂度是O(n^2),有没有O(n)的做法,当然有(´・ω・`)
因为大部分题都有求余,所以我们大可利用逆元的原理(没求余的题目,其实你也可以把MOD自己开的大一点,这样一样可以用逆元做)
根据这个公式
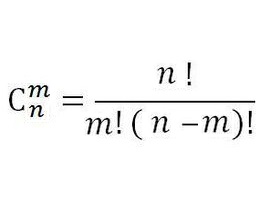 我们需要求阶乘和逆元阶乘
我们就用1e9+7来求余吧
费马小定理
a^(p-1) ≡1 (mod p)
两边同除以a
a^(p-2) ≡1/a (mod p)
数论1/a 是inv(a)
应该写a^(p-2) ≡ inv(a) (mod p)
所以inv(a) = a^(p-2) (mod p)
这个用快速幂求一下,复杂度O(logn)
引用其他人写的一句话
除法求模不能类似乘法,对于(A/B)mod C,直接(A mod C)/ (B mod C)是错误的;找到B的逆元b(b=B^-1);求出(A*b)modC即可;
由费马小定理:B 关于 P 的逆元为 B^(p-2);
费马小定理(Fermat Theory)是数论中的一个重要定理,其内容为: 假如p是质数,且gcd(a,p)=1,那么 a(p-1)≡1(mod p)。即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。所以,a^-1*a=1=a^(p-1),所以:a^-1=a^(p-2);
我们需要求阶乘和逆元阶乘
我们就用1e9+7来求余吧
费马小定理
a^(p-1) ≡1 (mod p)
两边同除以a
a^(p-2) ≡1/a (mod p)
数论1/a 是inv(a)
应该写a^(p-2) ≡ inv(a) (mod p)
所以inv(a) = a^(p-2) (mod p)
这个用快速幂求一下,复杂度O(logn)
引用其他人写的一句话
除法求模不能类似乘法,对于(A/B)mod C,直接(A mod C)/ (B mod C)是错误的;找到B的逆元b(b=B^-1);求出(A*b)modC即可;
由费马小定理:B 关于 P 的逆元为 B^(p-2);
费马小定理(Fermat Theory)是数论中的一个重要定理,其内容为: 假如p是质数,且gcd(a,p)=1,那么 a(p-1)≡1(mod p)。即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。所以,a^-1*a=1=a^(p-1),所以:a^-1=a^(p-2);数学排列组合公式:C(n,m)= n!/(m!*(n-m)!)
LL pow_mod(LL a, LL b, LL p){//a的b次方求余p
LL ret = 1;
while(b){
if(b & 1) ret = (ret * a) % p;
a = (a * a) % p;
b >>= 1;
}
return ret;
}
LL Fermat(LL a, LL p){//费马求a关于b的逆元
return pow_mod(a, p-2, p);
}
#include
#include
#include
using namespace std;
#define LL long long
#define G 1100000
#define mod 1000003
LL pri[G];
LL ni[G],ans;
LL pow(LL a,int b)
{
LL ans=1,base=a;
while (b>0)
{
if (b%2==1)
ans=(base*ans)%mod;
base=(base*base)%mod;
b/=2;
}
return ans;
}
void s() //打表
{
pri[0]=1;
ni[0]=1;
for (int i=1;i