• 向量的基本概念
• n维向量的模
• 向量点乘内积
• 向量投影
• 向量叉乘外积

转载请注明原始链接：http://blog.csdn.net/a464057216/article/details/54578170

向量的基本概念

向量和标量：“速度”和“位移”是向量，“速率”和“长度”是标量。几何上向量是有大小和方向的有向线段。始于tail，止于head：

向量描述事物间的位移和相对位置，向量不包括“位置”的概念。“点”有位置，但没有大小和厚度。
水平书写的向量叫行向量，垂直书写的向量叫列向量，列向量也可以采用行向量的转置记录，如[a b c]T。
负向量：每个向量v都有一个加性逆元-v，其维数与v一致且满足v+(-v) = 0。
向量加法的三角形法则：平移向量，使向量a的头连接向量b的尾，从a的尾到b的头的向量即为a+b。向量加法的三角形法则可以看作向量加法的几何学解释。

n维向量的模

向量的标准化即得到向量的单位向量的过程（向量除以它的模）。零向量不能被标准化！
单位向量：大小为1的向量，也叫标准化向量、法线。

向量点乘（内积）

向量点乘是对应分量乘积的和，结果是一个标量。点乘满足交换律，但是不满足结合律。
标量乘法、标量与向量的乘法可以省略乘号，但是向量和向量的点乘不能省略乘号。
点乘结果描述了两个向量相似的程度，点乘结果越大，两个向量约接近，θ是两个向量间的夹角：

通过a·b可以判断两个向量的夹角类型：结果大于0，夹角范围为[0, 90)；结果等于0，夹角等于90；结果小于0，夹角范围为(90, 180]。
零向量与任何向量均垂直。

向量投影

给定两个向量v和n，能将v分解成两个分量：v||和v⊥，分别平行和垂直于n，并满足v||+v⊥=v。称v||是v在n上的投影。

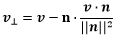
向量叉乘（外积）

两个向量做叉乘之后得到的是一个垂直于两个向量的向量。叉乘公式：

叉乘不满足交换律但是满足反交换律：a×b = -(b×a)。叉乘不满足结合律，即(a×b)×c ≠ a×(b×c)。 a×b的模等于向量的大小与向量夹角sin值的积，即a和b为边的平行四边形面积：

零向量与任何向量都平行。但是定义零向量平行或垂直任何向量是错误的，因为零向量没有方向。 a×b方向的确定：先让a的头与b的尾相接，在左手坐标系中，如果a和b呈顺时针，则a×b指向读者，如果呈逆时针，则a×b远离读者；在右手坐标系中正好相反，如果a和b呈顺时针，则a×b远离读者，如果呈逆时针，则a×b指向读者。

如果觉得我的文章对您有帮助，欢迎关注我(CSDN:Mars Loo的博客)或者为这篇文章点赞，谢谢!