Intersection

Time Limit: 4000/4000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 177    Accepted Submission(s): 76


Problem Description Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.


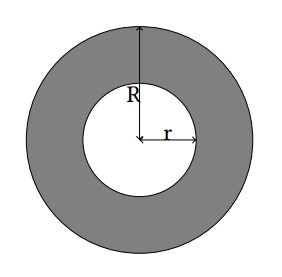
A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.


Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.  
Input The first line contains only one integer T (T ≤ 105), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers xi, yi (0 ≤ xi, yi ≤ 20) indicating the coordinates of the center of each ring.  
Output For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.
 
Sample Input 2 2 3 0 0 0 0 2 3 0 0 5 0  
Sample Output Case #1: 15.707963 Case #2: 2.250778  
Source 2014ACM/ICPC亚洲区北京站-重现赛（感谢北师和上交）




S： #include #include #include #include using namespace std; double w = 1e-8; double pi = acos(-1.0); struct node{ double x, y; }p, q; double f(node a,double r,node b,double R){ double d = sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); if(d >= r + R + w) return 0; if(fabs(R - r) + w >= d){ int rr = min(r, R); return pi * rr * rr; } double x = (r * r + d * d - R * R) / (2 * d); double g1 = acos(x / r); double g2 = acos((d - x) / R); return r * r * g1 + R * R * g2 - d * r * sin(g1); } int main(){ int T, k = 1; double ans; scanf("%d", &T); while(T--){ double x1, x2, y1, y2, r1, r2; scanf("%lf%lf%lf%lf%lf%lf", &r1, &r2, &x1, &y1, &x2, &y2); q.x = x1, q.y = y1; p.x = x2, p.y = y2; /* if(x1 == x2 && y1 == y2){ printf("Case #%d: %.6lf ", k++, ans); continue; } */ double ans = f(q, r2, p, r2) - f(q, r1, p, r2) - f(q, r2, p, r1) + f(q, r1, p, r1); printf("Case #%d: %.6lf ", k++, ans); } return 0; }